素数阶乘
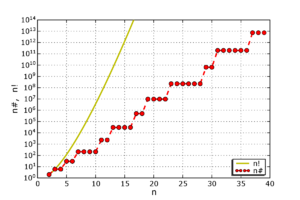
素数阶乘(又称:质数阶乘)是所有小于或等于该数的素数的积,自然数n的素数阶乘,写作n#。例如10以下的素数有:2,3,5,7,所以10# = 7×5×3×2 = 210。第n个素数阶乘的值,写作pn#。例:第三个素数为5,所以p3# = 5# = 5×3×2 = 30。[注 1] 素数阶乘与阶乘不同于,素数阶乘是素数乘积而阶乘是自然数乘积。 素数阶乘由Harvey Dubner定义并命名。
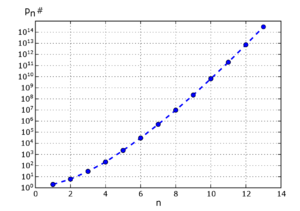
pn# 是计算第n个素数阶乘的函数
用素数定义
第n个素数pn的素数阶乘pn#定义为前n个素数的积:[1][2]
其中pk是第k个素数。
例如,p5#代表前五个素数的乘积:
前几个素数阶乘pn#是:
并定义p0# = 1 为空积。
素数阶乘pn#的渐进递增为:
其中:
用自然数定义
一般情况下,对于正整数n的一素数阶乘n#(或称作自然素数阶乘)也可以被定义为:[1][3]
其中,π(n)是素数计数函数(OEIS数列A000720),表示小于或等于某个实数n的素数的个数。
它等于:
- prime指素数,composite指合成数
例如,12# 代表素数≤ 12:
因为π(12) = 5,所以这个算式也可以写成:
前几个自然素数阶乘n#是:
不难发现当n为合成数时,n#的值总是与(n-1)#相同。例如上面提及的12# = p5# = 11#,因为12为合成数。
素数阶乘n#的渐进递增为:
素数阶乘的概念可以用于证明素数是无限的。(参见证明黎曼ζ函数的欧拉乘积公式)
恒等式
黎曼ζ函数在超过1的正整数可以素数阶乘与 Jordan's totient function 表示:
素数阶乘列表(部分)
| n | n# | pn | pn# |
|---|---|---|---|
| 0 | 1 | 无素数 | 1 |
| 1 | 1 | 2 | 2 |
| 2 | 2 | 3 | 6 |
| 3 | 6 | 5 | 30 |
| 4 | 6 | 7 | 210 |
| 5 | 30 | 11 | 2310 |
| 6 | 30 | 13 | 30030 |
| 7 | 210 | 17 | 510510 |
| 8 | 210 | 19 | 9699690 |
| 9 | 210 | 23 | 223092870 |
| 10 | 210 | 29 | 6469693230 |
| 11 | 2310 | 31 | 200560490130 |
| 12 | 2310 | 37 | 7420738134810 |
| 13 | 30030 | 41 | 304250263527210 |
| 14 | 30030 | 43 | 13082761331670030 |
| 15 | 30030 | 47 | 614889782588491410 |
参见
注释
- ^ 本段是翻译自日文"素数阶乘"条目
- ^ 本段(素数阶乘#用素数定义)是翻译自英文Primorial条目的"Definition for prime numbers"段落
- ^ 本段(素数阶乘#用自然数定义)是翻译自英文条目Primorial中的Definition for natural numbers段落
参考文献
- Harvey Dubner, "Factorial and primorial primes". J. Recr. Math., 19, 197–203, 1987.
- ^ 1.0 1.1 Weisstein, Eric W. (编). Primorial. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 2.0 2.1 2.2 Sloane, N.J.A. (编). Sequence A002110 (Primorial numbers (first definition): product of first n primes. Sometimes written prime(n)#). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N.J.A. (编). Sequence A034386 (Primorial numbers (second definition): n# = product of primes <= n.). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Weisstein, Eric W. (编). Chebyshev Functions. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).