Q指数是指数函数的Q模拟,定义如下
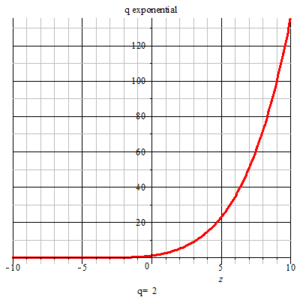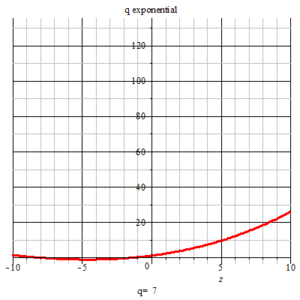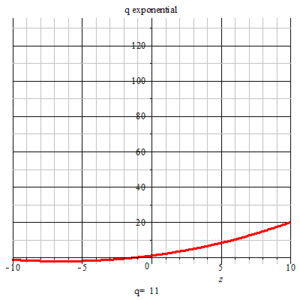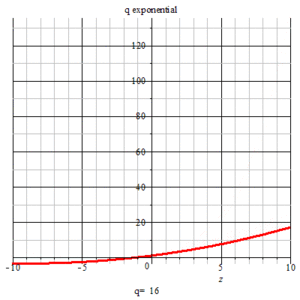
animation of q-exponential

其中
是 Q阶乘幂

![{\displaystyle \left({\frac {d}{dz}}\right)_{q}z^{n}=z^{n-1}{\frac {1-q^{n}}{1-q}}=[n]_{q}z^{n-1}.}](/media/math_img/1944/c5454c7904c36ab46a23fd93c086675aa4f7f618.svg)
关系式
当
-
其中, 是基本超几何函数的特例:
-
参考文献
- F. H. Jackson (1908), On q-functions and a certain difference operator, Trans. Roy. Soc. Edin., 46 253-281.
- Gasper G., and Rahman, M. (2004), Basic Hypergeometric Series, Cambridge University Press, 2004, ISBN 0521833574




![{\displaystyle \left({\frac {d}{dz}}\right)_{q}z^{n}=z^{n-1}{\frac {1-q^{n}}{1-q}}=[n]_{q}z^{n-1}.}](/media/math_img/1944/c5454c7904c36ab46a23fd93c086675aa4f7f618.svg)