此条目没有列出任何参考或来源。 (2019年1月9日)
维基百科所有的内容都应该可供查证。请协助补充可靠来源以改善这篇条目。无法查证的内容可能会因为异议提出而移除。 |
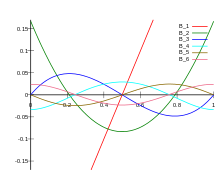
在数学中,伯努利多项式在对多种特殊函数特别是黎曼ζ函数和赫尔维茨ζ函数的研究中出现。作为阿佩尔序列的一种,与正交多项式不同的是,伯努利多项式的函数图像与x轴在单位长度区间内的交点数目并不会随着多项式次数的增加而增长。当多项式的次数趋近无穷大的时候,伯努利多项式的函数形状类似于三角函数。
表示法
伯努利多项式 Bn 有多种表示法,可视情况选用。
代数法
当 n ≥ 0 时,
-
其中bk 则为 伯努利数
函数法
伯努利多项式的母函数是
-
欧拉多项式母函数是
-
微分法
伯努利多项式亦可表示为微分的形式
-
其中 D = d/dx 是一个关于x的微分式,上述分式可以展开得到形式幂级数
-
积分法
伯努利多项式的多项式f可以通此积分方程求得
-
通过积分变换得到
-
多项式f 等价于
-
这可以用来求解伯努利多项式的反函数。