阿达马伽玛函数

在数学中，阿达马伽玛函数或阿达马的伽玛函数（Hadamard's gamma function）是除了伽玛函数之外的另一种阶乘的扩展定义方式，以雅克·阿达马命名。此函数可以视为将阶乘的参数向左平移1，并且在阶乘的非整数部分插值，但是有别于欧拉伽玛函数将阶乘扩展到实数和复数的定义。阿达马的伽玛函数的定义为：

阿达马伽玛函数

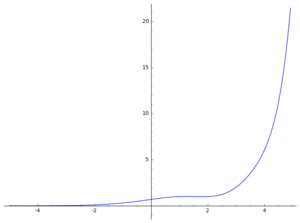
一般Γ函数与阿达马Γ函数

Γ函数（蓝色）、阿达马Γ函数（橘色），其值在正整数时相同

H(x)={\frac {1}{\Gamma (1-x)}}\,{\dfrac {d}{dx}}\left\{\ln \left({\frac {\Gamma ({\frac {1}{2}}-{\frac {x}{2}})}{\Gamma (1-{\frac {x}{2}})}}\right)\right\}

其中， $Γ(x)$ 是一般的伽玛函数。若 $n$ 为正整数，则其函数与伽玛函数和减一的阶乘相等：

H(n)=\Gamma (n)=(n-1)!\,

性质

阿达马伽玛函数与一般伽玛函数不同，阿达马伽玛函数没有奇点，是一个完全连续的函数，并且满足下面等式：

H(x+1)=x\,H(x)+{\frac {1}{\Gamma (1-x)}}

其中 ${\tfrac {1}{\Gamma (1-x)}}\to 0$ 在 $x$ 趋近正整数时趋近为0。


阿达马伽玛函数	一般伽玛函数
的复变函数图形


$\Gamma (x)-H(x)$	$\ln(\Gamma (x)-H(x))$	$\left\|\Gamma (x)-H(x)\right\|$	${\frac {H(x)}{\Gamma (x)}}$
阿达马伽玛函数与一般伽玛函数的关系由左至右分别为两函数的差、两函数之差的自然对数、两函数之差的绝对值以及两函数之比。绝对值越小颜色越深，红色是正实数、水蓝色是负实数可以看到在正整数的上两函数相等。

其他表示法

阿达马伽玛函数可以用双伽玛函数表示：

H(x)={\frac {\psi \left(1-{\frac {x}{2}}\right)-\psi \left({\frac {1}{2}}-{\frac {x}{2}}\right)}{2\,\Gamma (1-x)}}

H(x)=\Gamma (x)\left[1+{\frac {\sin(\pi x)}{2\pi }}\left\{\psi \left({\dfrac {x}{2}}\right)-\psi \left({\dfrac {x+1}{2}}\right)\right\}\right],

其中， $ψ(x)$ 表示双伽玛函数。

参考文献

Hadamard, M. J., Sur L’Expression Du Produit 1·2·3· · · · ·(n−1) Par Une Fonction Entière (PDF), OEuvres de Jacques Hadamard, Centre National de la Recherche Scientifiques, Paris, 1968, 1894 [2018-11-25], （原始内容存档 (PDF)于2021-02-25）（法语）
Srivastava, H. M.; Junesang, Choi. Zeta and Q-Zeta Functions and Associated Series and Integrals. Elsevier insights. 2012: 124. ISBN 0123852188.
Introduction to the Gamma Function. The Wolfram Functions Site. Wolfram Research, Inc. [27 February 2016]. （原始内容存档于2021-05-07）.