五维多胞体
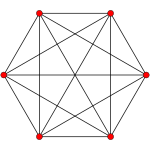 五维正六胞体 |
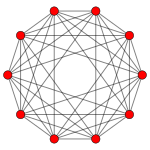 五维正轴体, 211 |
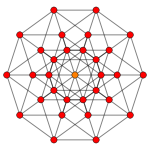 五维超正方体 |
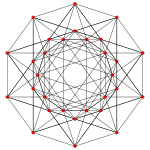 扩展五维正六胞体 |
 截半五维正轴体 |
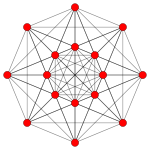 五维半立方体 121 |
在五维几何学中,五维多胞体又称5-多胞形,是由多个四维多胞体作为维面所构成的封闭几何结构,每个四维胞中的三维胞(多面体)都是2个四维胞的公共胞。
这些多胞体的组成元素可分为四维胞、三维胞、面、棱和顶点,其中四维胞又称为此几何结构的维面;三维胞又称为此几何结构的维棱;二维的面又称为此几何结构的维峰,维面、维脊和维峰可以视为三维多面体之面、棱和顶点在五维多胞体的类比。
五维空间中至少需具有6个四维胞才能构成不退化的五维多胞体,为六胞体。而四维胞数最少的五维正多胞体亦由6个四维胞组成,称为五维正六胞体,由6个全等的四维正五胞体组成。
定义
五维多胞体是位于五维空间的封闭几何结构,组成元素包括了顶点、边、面、三维胞和四维胞,每个顶点都至少是五条边的公共顶点;每条边都至少是四个面的公共边;每个面也都至少是三个多面体胞的公共面,其三维胞要是不退化的多面体;维面(或四维胞)也要是不退化的四维多胞体。
此外,也需满足下列条件:
- 每个多面体胞要恰好连接2个四维胞
- 类似三维多面体中的“两条棱要恰好连接2个面”
- 相邻的四维胞不能位于同一个四维空间中
- 类似三维多面体中的“两个相邻面不得共面”,在三维多面体中则可换句话说“两个相邻面不得位于同一个二维空间中”
- 该几何结构不是复合体
- 在三维多面体中,星形八面体则为复合体,由2个正四面体组成;在二维多边形中大卫之星则为复合图形,由2个正三角形组成。
以五维超正方体为例:
- 每个正方体胞恰好连接2个超立方体维面。
- 相邻的超立方体维面所在的四维空间互相垂直
- 类似三维立方体中的“相邻两正方形所在平面互相垂直”
- 五维超正方体并不是由2种几何形状组合而成。
- 例如“二复合五维正六胞体”即为复合体,并且是大卫之星、星形八面体在五维空间中的类比,其只能视为复合图形,并非一个简单多胞体。
因此五维超正方体是一种五维多胞体。
性质
任一五维多胞体,其拓朴结构可以由其扭转系数和贝蒂数定义[1]。
用于表征多面体的欧拉特征数无法十分有效地推广到四维或更高维度,换句话说,即欧拉特征数无法有效地区分在五维空间中的五维多胞体之不同拓扑结构,由于欧拉特征数不足以可靠地区分更高维度的不同拓扑结构导致发现了更复杂的贝蒂数[1]。
正多胞体
五维空间中共存在三种凸正多胞体,即五维空间只有三种凸的有限几何结构满足所有四维胞全等、三维胞全等、面全等、所有棱等长、所有角等角的特性。
五维空间的正多胞体在施莱夫利符号中皆可以用{p,q,r,s}表示,代表每个二维的面都是s个{p,q,r}四维胞的公共面。
三种五维凸正多胞体的施莱夫利符号分别为:
这些正多胞体的四维胞、三维胞、面、棱和顶点的数量分别为:
| 名称 | 施莱夫利符号 | 考克斯特记号 | 顶点 | 边 | 面 | 三维胞 | 四维胞 | 对称性 (阶数) |
|---|---|---|---|---|---|---|---|---|
| 五维正六胞体 | {3,3,3,3} | 6 | 15 | 20 | 15 | 6 | A5, (120) | |
| 五维超正方体 | {4,3,3,3} | 32 | 80 | 80 | 40 | 10 | BC5, (3820) | |
| 五维正轴体 | {3,3,3,4} {3,3,31,1} |
|
10 | 40 | 80 | 80 | 32 | BC5, (3840) 2×D5 |
均匀多胞体
在五维几何学中,五维均匀多胞体或五维半正多胞体是指具有点可递的五维多胞体。[2]
其中三种五维半正多胞体的四维胞、三维胞、面、棱和顶点的数量分别为:
| 名称 | 施莱夫利符号 | 考克斯特记号 | 顶点 | 边 | 面 | 三维胞 | 四维胞 | 对称性 (阶数) |
|---|---|---|---|---|---|---|---|---|
| 扩展五维正六胞体 | t0,4{3,3,3,3} | 30 | 120 | 210 | 180 | 162 | 2×A5, (240) | |
| 五维半立方体 | {3,32,1} h{4,3,3,3} |
|
16 | 80 | 160 | 120 | 26 | D5, (1920) ½BC5 |
| 截半五维正轴体 | t1{3,3,3,4} t1{3,3,31,1} |
|
40 | 240 | 400 | 240 | 42 | BC5, (3840) 2×D5 |
参考文献
- ^ 1.0 1.1 Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy, Princeton, 2008.
- ^ Klitzing, Richard. 5D uniform polytopes (polytera). bendwavy.org.
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1](页面存档备份,存于互联网档案馆)
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. 5D uniform polytopes (polytera). bendwavy.org.
外部链接
- Polytopes of Various Dimensions(页面存档备份,存于互联网档案馆), Jonathan Bowers
- Uniform Polytera(页面存档备份,存于互联网档案馆), Jonathan Bowers
- Multi-dimensional Glossary(页面存档备份,存于互联网档案馆), Garrett Jones