七维正八胞体
在几何学中,七维正八胞体(Octaexon或Octa-7-tope)是一种自身对偶的正七维多胞体[1],是七维空间的单纯形也是七维空间中最简单的正图形,因此又称为7-单纯形(7-simplex)[2]:127 ,由8个六维正七胞体的六维胞组成,其二面角为cos−1(1/7)约为81.79°[1]。乔纳森·鲍尔斯(Jonathan Bowers)将七维正八胞体缩写为oca[3]。
| 正八胞体 | |
|---|---|
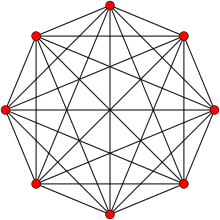 | |
| 类型 | 正七维多胞体 八胞体 |
| 家族 | 单纯形 |
| 维度 | 七维 |
| 对偶多胞形 | 七维正八胞体(自身对偶) |
| 识别 | |
| 鲍尔斯缩写 | oca |
| 数学表示法 | |
| 考克斯特符号 | |
| 施莱夫利符号 | {3,3,3,3,3,3} {36} |
| 性质 | |
| 六维胞 | 8个六维正七胞体 |
| 五维胞 | 28个五维正六胞体 |
| 四维胞 | 56个正五胞体 |
| 胞 | 70个正四面体 |
| 面 | 56个正三角形 |
| 边 | 28 |
| 顶点 | 8 |
| 欧拉示性数 | 2 |
| 特殊面或截面 | |
| 皮特里多边形 | 正八边形 |
| 组成与布局 | |
| 顶点图 | 六维正七胞体 |
| 对称性 | |
| 对称群 | A7 [3,3,3,3,3,3] |
| 特性 | |
| 凸 | |
性质
七维正八胞体共由8个顶点、28条边、56个三角形面、70个正四面体的三维胞、56个正五胞体的四维胞、28个五维正六胞体的五维胞和8个六维正七胞体的六维胞组成,其中六维正七胞体为七维正八胞体的维面。对于一个边长为a的七维正八胞体,其超胞积是 ,表胞积是 ,高是 。若一个七维正八胞体的棱长为1,则其外接七维超球的半径为 ,内切七维超球的半径为 。[1]
边长为2的七维正八胞体可以内接于单位七维超立方体中。[4]下一个可以内接于单位超方形的最大单纯形为十一维正十二胞体。[5]
作为一种排布
七维正八胞体的排布矩阵为:[1]
行和列对应于七维正八胞体的顶点、边、面、胞、四维胞、五维胞和六维胞。对角线上的数字表示该元素在七维正八胞体中的数量。非对角线的数量表示对应行所代表的元素上有多少列所代表的元素交于该处。由于七维正八胞体是一种自身对偶的多胞体,因此这个排布矩阵旋转180度后会相同。[6][7]
顶点坐标
若一个七维正八胞体几何中心位于原点,且边长为2单位长,则其顶点坐标为:
透过将七维正八胞体可以内接于七维超立方体中可以获得更简单的坐标集合,其值为:[1]
更简单地,七维正八胞体可以坐落于八维空间坐标(0,0,0,0,0,0,0,1)的排列。这个结构是基于八维正轴体的维面。
图像
| 三维空间的七维正八胞体 | ||||||
| 三角化四面体包络中的球棍模型 |
以振幅多面体表面呈现的七维正八胞体 |
七维正八胞体投影到三维,再用相机投影示意其皮特里投影 | ||||
正交投影
| Ak考克斯特平面 | A7 | A6 | A5 |
|---|---|---|---|
| 图像 | |||
| 二面体群对称性 | [8] | [7] | [6] |
| Ak考克斯特平面 | A4 | A3 | A2 |
| 图像 | |||
| 二面体群对称性 | [5] | [4] | [3] |
参考文献
- ^ 1.0 1.1 1.2 1.3 1.4 Klitzing, Richard. octaexon. bendwavy.org. [2022-12-19]. (原始内容存档于2022-12-19).
- ^ Klitzing, Richard. 7D uniform polytopes (polyexa) x3o3o3o3o3o3o — oca. bendwavy.org.
- ^ Adams, Joshua; Zvengrowski, Peter; Laird, Philip. Vertex Embeddings of Regular Polytopes. Expositiones Mathematicae. 2003.
- ^ Sloane, N.J.A. (编). Sequence A019442. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
Integers n such that a simplex of dimension n-1 can be inscribed in a hypercube of dimension n-1
- ^ Coxeter, H.S.M. §1.8 Configurations. Regular Polytopes 3rd. Dover. 1973. ISBN 0-486-61480-8.
- ^ Coxeter, H.S.M. Regular Complex Polytopes 2nd. Cambridge University Press. 1991: 117 [2022-12-19]. ISBN 9780521394901. (原始内容存档于2023-01-09).