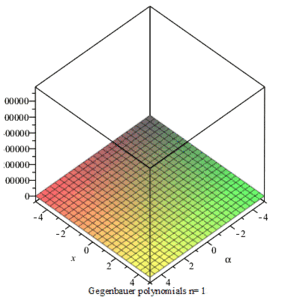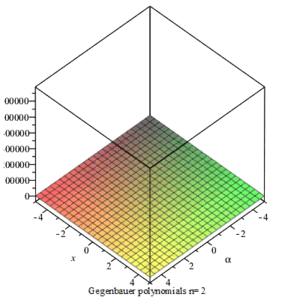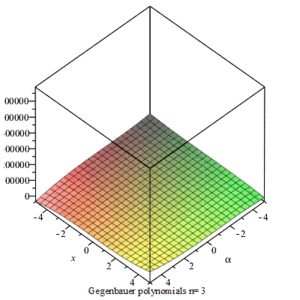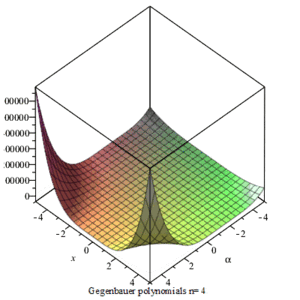
性质
盖根鲍尔多项式具有若干性质:
-
-
-
- 当 α = 1/2, 方程约化为勒让德方程, 盖根鲍尔多项式约化为勒让德多项式.
-
- (Abramowitz & Stegun p. 561 (页面存档备份,存于互联网档案馆)). 其中(2α)n 为上升阶乘幂. 具体来说,
-
-
- 因而满足罗德里格公式
-
正交归一性
当n ≠ m时,对于固定的α和权函数
- ,
盖根鲍尔多项式在区间[−1, 1]上加权正交 (Abramowitz & Stegun p. 774 (页面存档备份,存于互联网档案馆))
-
归一性:
-
应用
盖根鲍尔多项式作为勒让德多项式的扩展经常出现在势理论和谱分析中. Rn空间中的牛顿势可以在α = (n − 2)/2情况下展开为盖根鲍尔多项式,
-
当n = 3, 可以得到引力势的勒让德展开。类似的表达式还有球中泊松核的展开(Stein & Weiss 1971).
当只考虑x时, 为球谐函数。
盖根鲍尔多项式在正定函数理论中亦有涉及。
另见
参考文献
- Abramowitz, Milton; Stegun, Irene Ann (编). Chapter 22. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series 55 Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first. Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. 1983: 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Bayin, S.S., Mathematical Methods in Science and Engineering, Wiley, 2006 , Chapter 5.
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F., Orthogonal Polynomials, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248
- Stein, Elias; Weiss, Guido, Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, 1971, ISBN 978-0-691-08078-9 .
- Suetin, P.K., Ultraspherical polynomials, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 .

![[-1,1]](/media/math_img/2040/51e3b7f14a6f70e614728c583409a0b9a8b9de01.svg)