哈恩多项式是一个以德国数学家Wolfgang Hahn命名的正交多项式,由下列广义超几何函数定义:[1]

前几个哈恩多项式为
![{\displaystyle h[5]:=1+27*x/(-4*\alpha -4)+3*x*\alpha /(-4*\alpha -4)+270*x^{2}/((-4*\alpha -4)*(-3*\alpha -6))+57*x^{2}*\alpha /((-4*\alpha -4)*(-3*\alpha -6))-270*x/((-4*\alpha -4)*(-3*\alpha -6))-57*x*\alpha /((-4*\alpha -4)*(-3*\alpha -6))+3*x^{2}*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6))-3*x*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6))+990*x^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+299*x^{3}*\alpha /((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-2970*x^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-897*x^{2}*\alpha /((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+30*x^{3}*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-90*x^{2}*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+1980*x/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+598*x*\alpha /((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+60*x*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+x^{3}*\alpha ^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-3*x^{2}*\alpha ^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+2*x*\alpha ^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))}](/media/math_img/2042/348f195746807fb782e5e4e8942a9c1a9e462d95.svg)
![{\displaystyle h[6]:=1+27*x/(-5*\alpha -5)+3*x*\alpha /(-5*\alpha -5)+270*x^{2}/((-5*\alpha -5)*(-4*\alpha -8))+57*x^{2}*\alpha /((-5*\alpha -5)*(-4*\alpha -8))-270*x/((-5*\alpha -5)*(-4*\alpha -8))-57*x*\alpha /((-5*\alpha -5)*(-4*\alpha -8))+3*x^{2}*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8))-3*x*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8))+990*x^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+299*x^{3}*\alpha /((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-2970*x^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-897*x^{2}*\alpha /((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+30*x^{3}*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-90*x^{2}*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+1980*x/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+598*x*\alpha /((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+60*x*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+x^{3}*\alpha ^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-3*x^{2}*\alpha ^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+2*x*\alpha ^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9)).}](/media/math_img/2042/69119846cc8c8ae77c3c21c7f247b32293791883.svg)
正交性
对于 > -1 和 > -1 以及 < -N
< -N,下列正交关系成立[2]
归递关系
哈恩多项式满足下列归递关系[3] = - *
其中
极限关系
- 拉卡多项式→哈恩多项式[4]
-
- 哈恩多项式→雅可比多项式
参考文献
- ^ Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14)
- ^ Roelof Koekoek, p204
- ^ Roelof KoeKoek p204
- ^ Roelof,p206-207
- Roelof Koekoek, Peter A.Lesky,ReneF.Swarttouw,Hypergeometric Orthogonal Polynomials ad Their q=Aalogues, Springer,2008.
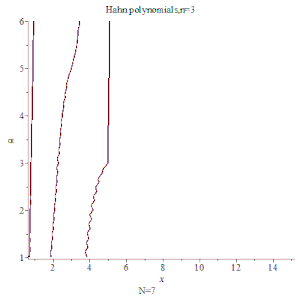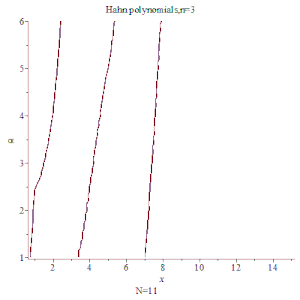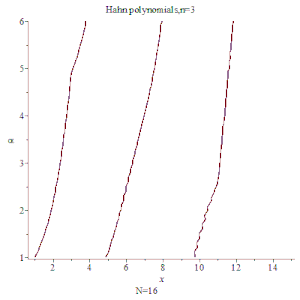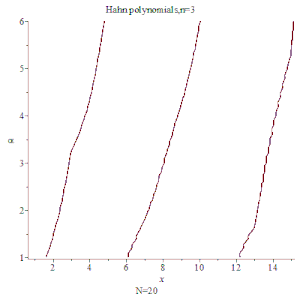

![{\displaystyle h[5]:=1+27*x/(-4*\alpha -4)+3*x*\alpha /(-4*\alpha -4)+270*x^{2}/((-4*\alpha -4)*(-3*\alpha -6))+57*x^{2}*\alpha /((-4*\alpha -4)*(-3*\alpha -6))-270*x/((-4*\alpha -4)*(-3*\alpha -6))-57*x*\alpha /((-4*\alpha -4)*(-3*\alpha -6))+3*x^{2}*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6))-3*x*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6))+990*x^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+299*x^{3}*\alpha /((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-2970*x^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-897*x^{2}*\alpha /((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+30*x^{3}*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-90*x^{2}*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+1980*x/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+598*x*\alpha /((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+60*x*\alpha ^{2}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+x^{3}*\alpha ^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))-3*x^{2}*\alpha ^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))+2*x*\alpha ^{3}/((-4*\alpha -4)*(-3*\alpha -6)*(-2*\alpha -6))}](/media/math_img/2042/348f195746807fb782e5e4e8942a9c1a9e462d95.svg)
![{\displaystyle h[6]:=1+27*x/(-5*\alpha -5)+3*x*\alpha /(-5*\alpha -5)+270*x^{2}/((-5*\alpha -5)*(-4*\alpha -8))+57*x^{2}*\alpha /((-5*\alpha -5)*(-4*\alpha -8))-270*x/((-5*\alpha -5)*(-4*\alpha -8))-57*x*\alpha /((-5*\alpha -5)*(-4*\alpha -8))+3*x^{2}*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8))-3*x*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8))+990*x^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+299*x^{3}*\alpha /((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-2970*x^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-897*x^{2}*\alpha /((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+30*x^{3}*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-90*x^{2}*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+1980*x/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+598*x*\alpha /((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+60*x*\alpha ^{2}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+x^{3}*\alpha ^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))-3*x^{2}*\alpha ^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9))+2*x*\alpha ^{3}/((-5*\alpha -5)*(-4*\alpha -8)*(-3*\alpha -9)).}](/media/math_img/2042/69119846cc8c8ae77c3c21c7f247b32293791883.svg)