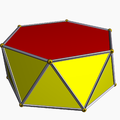
六方偏方面体
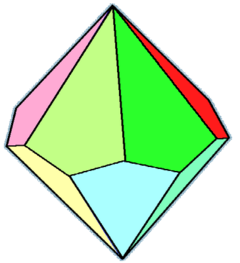
在几何学中,六方偏方面体是一个由12个全等的筝形组成的多面体,是十二面体的一种,同时也是筝形多面体。其对偶多面体为六角反棱柱。在化学中,原子的晶体结构可以在空间中以六方偏方面体形状的胞重复排列。[1]
 | ||
| 类别 | 偏方面体 | |
|---|---|---|
| 对偶多面体 | 六角反棱柱 | |
| 数学表示法 | ||
| 考克斯特符号 | ||
| 性质 | ||
| 面 | 12 | |
| 边 | 24 | |
| 顶点 | 14 | |
| 欧拉特征数 | F=12, E=24, V=14 (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 12个筝形 | |
| 面的布局 | V6.3.3.3 | |
| 对称性 | ||
| 对称群 | D6d, [2+,12], (2*6), 24阶 | |
| 旋转对称群 | D6, [2,6]+, (226), order 12 | |
| 特性 | ||
| 凸、面可递 | ||
| 图像 | ||
| ||
性质
六方偏方面体共由12个面、24条边和14个顶点组成。组成六方偏方面体的12个面都是筝形,而组成六方偏方面体的14个顶点有2个是6个筝形的公共顶点,另外12个是3个筝形的公共顶点。[2]
变体
| 种类 | 扭曲的梯形、等面 | 不等面 | 不等面且扭曲 | |
|---|---|---|---|---|
| 对称性 | D6, (662), [6,2]+, 12阶 | C6v, (*66), [6], 12阶 | C6, (66), [6]+, 6阶 | |
| 图像 (n=6) |
||||
| 展开图 | ||||
相关多面体
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|
| |
|
|
|
|
|
|
|
|
|
|
|
| 球面投影 | |||||||||||
| 对称群:[6,2], (*622) | [6,2]+, (622) | [1+,6,2], (322) | [6,2+], (2*3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| {6,2} | t{6,2} | r{6,2} | 2t{6,2}=t{2,6} | 2r{6,2}={2,6} | rr{6,2} | tr{6,2} | sr{6,2} | h{6,2} | s{2,6} |
| 半正对偶 | |||||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V32 | V3.3.3.3 |
参考文献
- ^ 3 2 and Hexagonal-trapezohedric Class, 6 2 2. [2019-09-29]. (原始内容存档于2019-03-20).
- ^ Dipyramids & Trapezohedra: Hexagonal Trapezohedron. dmccooey.com. [2022-12-29]. (原始内容存档于2022-12-29).