二面体

部分的二面体
Torus square tiling 2x1.png
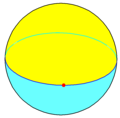环形二面体{4,4}1,1		 Hengonal dihedron.png
一角形二面体
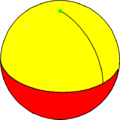Spherical henagonal pyramid.png
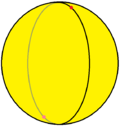一角锥 		Spherical digonal hosohedron.png
二面形

在几何学中，二面体是指由2个面组成的多面体，但由于三维空间中的多面体至少要具有4个面，因此少于四个面的多面体只能是退化的，换句话说，小于4个面的多面体无法具有非零的体积。二面体中最常见的就是多边形二面体，即由两个全等的平面图型封闭出的零体积空间所形成的退化多面体。最简单的二面体是一种球面镶嵌：一角形二面体，它的对偶是一面形。另外二面体也可以以环形多面体（英语：Toroidal polyhedron）或正则地区图的形式存在。

二面体中不存在任何柱体，因为如果柱体要仅有两个面，代表其不存在侧面，而这样的立体就不是柱体了。

常见的二面体

平面图形

主条目：多边形二面体

任何平面图形都可以视为一个二面体，并且属于二面体群。

若将一封闭的平面图形放置于三维空间也可以视为一个二面体，如多边形二面体。他们皆属于二面体群，是透镜空间（英语：Lens_space）的基本域[1]。

球面镶嵌

二面体可以以球面镶嵌的方式存在，最简单的例子是二面形。

名称 二面形 一角形二面体 多边形二面体
图像      
施莱夫利符号 {2,2} {1,2}
h{2,2} 		{n,2}
考克斯特记号                  

二面形

主条目：多面形

一个二面形，是一种由二个镶嵌在球体上的球弓形组成的多面形，施莱夫利符号中利用{2,2}来表示，该符号表达了二面形的结构——每个顶点都是2个二角形的公共顶点。

一角形二面体

 
球面上的一角形二面体

一角形二面体，又称为双一角形（dimonogon[2]）是一种退化的多边形二面体，由2个一角形组成，这个几何结构只有1个顶点，该顶点为2个一角形的公共顶点，在施莱夫利符号中用{1,2}表示，其具有2个面、1条边和1个顶点，对偶多面体是一个一面体：一面形。[2]

在球面几何学中，一角形二面体是一个球面上的一个圆上任一顶点。这形成了一个二面体，施莱夫利符号中利用{1,2}来表示，与的两个半球形一角形面，共用一个360°的边和一个顶点。它的对偶是一面形，施莱夫利符号中利用{2,1}来表示，具有一个二角形面（一个完整的360°弓形），一个180°的边缘，和两个顶点，因此属于一面体。

一角形二面体可以截角为三面形[2][3]。

 
作为正则地区图的一角形二面体。两个面分别以蓝色和黄色表示 		 
截角的一角形二面体，红色为截角的截面，所形成的立体为三面形

一角锥

 
作为球面镶嵌的一角锥

一角锥是指底面为一角形的锥体，由于其底面为一角形，因此在欧几里得空间中，其已经退化无法拥有体积。在球面几何学中，其可以作为球面镶嵌，此时的一角锥由1个球面一角形和1个球面三角形构成。这种一角锥共有2个面、2条边和2个顶点。一角锥的对偶多面体同样是一角锥，因此是一种自身对偶的多面体。

双一角锥

双一角锥是以一角形为底的双锥体，为一角柱的对偶多面体。由于其以一角形为底，因此在欧几里得空间中，其已经退化无法拥有体积。在球面几何学中，其可以作为球面镶嵌，这种双一角锥由2个面、3条边和3个顶点组成，其两个面都是三角形，但拓扑结构与三角形二面体不同，其中的两个顶点为对跖点，剩下的一个顶点位于赤道面上连结与对跖点相连的两条边。双一角锥的对偶多面体为一角柱。

环形多面体

 
{4,4}1,1是一种在环面由两个两两共用顶点的四边形组成

部分的环形多面体也是二面体，例如{4,4}1,1是一种环形二面体[5]，为环面上的两个四边形面共用2个顶点和4条边；以及{3,6}1,0也是一种环面二面体，为环面上两个三角形共用一个顶点和三条边。

正则地区图

部分的正则地区图由两个面组成，可以视为二面体的一种，例如亏格为2的二面正则地区图有S2:{8,4}、S2:{6,6}和S2:{5,10}。其中S2:{8,4}为由两个八边形面共用4个顶点和8条边[6]，并且八边形在顶点周围自我重复相邻两次，也就是顶点周围围绕着4个八边形，且对应的皮特里多边形为八边形，因此其在施莱夫利符号中可以用{8,4}8来表示[7]；S2:{6,6}为由两个六边形共用两个顶点和6条边[8]，并且六边形在顶点周围自我重复相邻三次，也就是其顶点周围围绕着六个六边形，且对应的皮特里多边形为二角形，因此在施莱夫利符号中可以用{6,6}2来表示[7]；S2:{5,10}为由两个五边形共用一个顶点和5条边[9]，并且五边形在顶点周围自我重复相邻五次，也就是其顶点周围围绕着10个五边形，且对应的皮特里多边形为二角形，因此在施莱夫利符号中可以用{5,10}2来表示[7]。

亏格 名称 施莱夫利符号 顶点 边 面 组成面 顶点图 皮特里多边形 对偶
2[7] S2:{8,4} {8,4}8 4 8 2 八边形 四边形（4个八边形的公共顶点） 八边形 S2:{4,8}（4个面）
S2:{6,6} {6,6}2 2 6 2 六边形 六边形（6个六边形的公共顶点） 二角形 自身对偶
S2:{5,10} {5,10}2 1 5 2 五边形 十边形（10个五边形的公共顶点） 二角形 S2:{10,5}（1个面）
3[10] S3:{12,4} {12,4}6 6 12 2 十二边形 四边形（4个十二边形的公共顶点） 六边形 S3:{4,12}（6个面）
S3:{8,8}4 {8,8}4 2 8 2 八边形 八边形（8个八边形的公共顶点） 四边形 自身对偶[11][12]
S3:{8,8}2 {8,8}2 二角形
S3:{7,14} {7,14}2 1 7 2 七边形 十四边形（14个七边形的公共顶点） 二角形 S3:{14,7}（1个面）
4[13] S4:{16,4} {16,4}16 8 16 2 十六边形 四边形（4个十六边形的公共顶点） 十六角形 S4:{4,16}（8个面）
S4:{12,6} {12,6}4 4 12 2 十二边形 六边形（6个十二边形的公共顶点） 四边形 S4:{6,12}（4个面）
S4:{10,10} {10,10}2 2 10 2 十边形 十边形（10个十边形的公共顶点） 二角形 自身对偶
S4:{9,18} {9,18}2 1 9 2 九边形 十八边形（18个九边形的公共顶点） 二角形 S4:{18,9}（1个面）

圆锥

主条目：圆锥

在不严谨的情况下，圆锥也能算是一种二面体，因为它可以看做是只有两个面的几何体，由一曲面（侧面）和一圆形平面（底面）所组成。

二面体列表

名称 种类 图像 符号 顶点 边 面 χ 面的种类 对称性
一角形二面体 多边形二面体   {1,2}
    		1 1 2 2 2个一角形  C1v
（*22）
二面形 多面形
多边形二面体 		  {2,2}
      		2 2 2 2 2个二角形  D2h
（*222）
一角锥 角锥
退化多面体
球面多面体 		  ( )∨{1} 2 2 2 2 1个一角形
1个三角形 		C1v, [1]
双一角锥 双锥体
退化多面体
球面多面体 		  { }+{1} 3 3 2 2 2个三角形 D1h, [1,2], (*221) order 4
四面形半形
（hemi-4-hosohedron）[14]		 多面形
多面体半形 		{2,4}4/2 1 2 2 1 2个二角形 
三维多边形 多边形二面体   {n,2}
      		n n 2 2 2个全等的多边形  Dnh
（*n22）
二阶无限边形镶嵌[16] 镶嵌图   {∞,2}
     
      		∞ ∞ 2 2 2个无限边形  [∞,2], (*∞22)
{4,4}1,1 环形多面体   {4,4}1,1 2 4 2 0 2个正方形 
{3,6}1,0 环形多面体   {3,6}1,0 1 3 2 0 2个正三角形 
S2:{8,4}[6] 正则地区图 {8,4}8[7] 4 8 2 -2 2个八边形
S2:{6,6}[8] 正则地区图 {6,6}2[7] 2 6 2 -2 2个六边形
S2:{5,10}[9] 正则地区图 {5,10}2[7] 1 5 2 -2 2个五边形
圆锥体 非严格多面体
曲面
柱体 		  1 1 2 2 1个曲面
1个圆形

参见

参考文献

  1. ^ Gausmann, Evelise; Roland Lehoucq, Jean-Pierre Luminet, Jean-Philippe Uzan, Jeffrey Weeks. Topological Lensing in Spherical Spaces. Classical and Quantum Gravity. 2001, 18: 5155–5186. arXiv:gr-qc/0106033  . doi:10.1088/0264-9381/18/23/311. 
  2. ^ 2.0 2.1 2.2 The dimonogon. weddslist.com. [2022-12-15]. （原始内容存档于2021-07-31）. 
  3. ^ The 3-hosohedron. weddslist.com. [2022-12-15]. （原始内容存档于2022-12-15）. 
  4. ^ Coxeter, H. S. M.; Moser, W. O. J., Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete 14 4th, Springer Verlag, 1980, ISBN 978-0-387-09212-6 
  5. ^ Coxeter 1980 [4], 8.3 Maps of type {4,4} on a torus.
  6. ^ 6.0 6.1 S2:{8,4}. weddslist.com. [2022-12-15]. 
  7. ^ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 Regular maps in the orientable surface of genus 2. weddslist.com. [2022-12-15]. （原始内容存档于2022-11-29）. 
  8. ^ 8.0 8.1 S2:{6,6}. weddslist.com. [2022-12-15]. 
  9. ^ 9.0 9.1 S2:{5,10}. weddslist.com. [2022-12-15]. 
  10. ^ Regular maps in the orientable surface of genus 3. weddslist.com. [2022-12-15]. （原始内容存档于2021-10-19）. 
  11. ^ S3:{8,8}4. weddslist.com. [2022-12-15]. 
  12. ^ S3:{8,8}2. weddslist.com. [2022-12-15]. 
  13. ^ Regular maps in the orientable surface of genus 4. weddslist.com. [2022-12-15]. （原始内容存档于2021-10-19）. 
  14. ^ The hemi-4-hosohedron. weddslist.com. [2022-12-15]. （原始内容存档于2020-02-01）. 
  15. ^ The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
  16. ^ Conway (2008)[15], p. 263