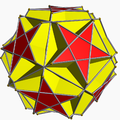
大星形五角化十二面体

大星形五角化十二面体由60个面、90条边和32个顶点组成^[4]，是一种六十面体。其具有互相相交的面，是一种复杂多面体，但其仅有面互相相交，其所有面都是凸多边形^[4]。

面的组成

大星形五角化十二面体的面由60个全等的等腰钝角三角形组成，每个等腰顿角三角形彼此互相相交，每个等腰三角形皆露出两个顿角三角形部分，其余皆隐藏于该立体的内部。露在该立体外部的部分如下图，以蓝色表示，其中黑线代表等腰顿角三角形彼此互相相交的位置：

大星形五角化十二面体一共有两种边长，分别为等腰三角形的底边，和等腰三角形的腰长。 若其对偶多面体截角大二十面体的边长为单位长，则等腰三角形的腰长为^[5]：

${\displaystyle {\frac {9(1+2{\sqrt {5}})}{19}}\approx 2.592}$ 

在同样情况下，等腰三角形的底边长为^[5]：

${\displaystyle {\frac {3(1+{\sqrt {5}})}{2}}\approx 4.8541}$ 

二面角

大星形五角化十二面体的二面角仅有一种，其值为^[5]：

${\displaystyle \cos ^{-1}(-{\frac {80-9{\sqrt {5}}}{109}})\approx 2.15234\approx 123.32^{\circ }}$ 

顶点坐标

若一个大星形五角化十二面体几何中心位于原点，且其经对偶变换后的立体边长为1单位长，则其顶点坐标为^[6]：

${\displaystyle (\pm {\frac {3(1+{\sqrt {5}})}{4}},0,\pm {\frac {3({\sqrt {5}}-1)}{4}})}$ 、

${\displaystyle (0,\pm {\frac {3({\sqrt {5}}-1)}{4}},\pm {\frac {3(1+{\sqrt {5}})}{4}})}$ 、

${\displaystyle (\pm {\frac {3({\sqrt {5}}-1)}{4}},\pm {\frac {3(1+{\sqrt {5}})}{4}},0)}$ 、

${\displaystyle (0,\pm {\frac {9(9-{\sqrt {5}})}{76}},\pm {\frac {9(5{\sqrt {5}}-7)}{76}})}$ 、

${\displaystyle (\pm {\frac {9(9-{\sqrt {5}})}{76}},\pm {\frac {9(5{\sqrt {5}}-7)}{76}},0)}$ 、

${\displaystyle (\pm {\frac {9(5{\sqrt {5}}-7)}{76}},0,\pm {\frac {9(9-{\sqrt {5}})}{76}})}$ 、

${\displaystyle (\pm {\frac {3}{2}},\pm {\frac {3}{2}},\pm {\frac {3}{2}})}$ 。

对偶复合体

对偶复合体，即一个多面体与其对偶多面体组合成的复合图形。大星形五角化十二面体与其对偶的复合体为复合截角大二十面体大星形五角化十二面体。其共有92个面、180条边和92个顶点，其尤拉示性数为4，亏格为-1，有12个非凸面^[7]。

• 大星形十二面体

• 埃里克·韦斯坦因. 大星形五角化十二面體. MathWorld.