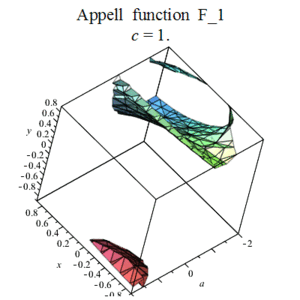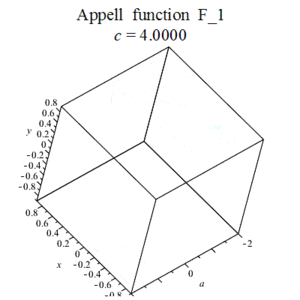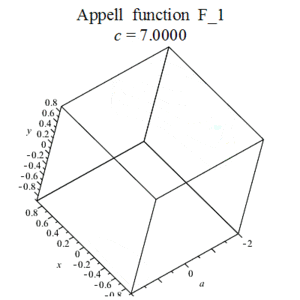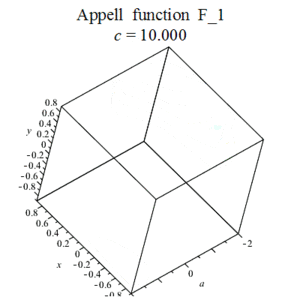
阿佩尔函数是法国数学家(Paul Apell)在1880年为推广高斯超几何函数而创建的一组双变数函数,定义如下




其中的符号 是阶乘幂
是阶乘幂
阿佩尔函数是嫪丽切拉函数和Kampé_de_Fériet函数的特例。
归递关系
-
-
-
-
其它式子[1]可从这四个关系导出。
-
-
-
-
-
导数与微分方程
-
-
-
-
-
-
-
-
积分关系
-
特例
-
-
-
参见
参考文献
- ^ 例如:
- Appell, Paul. Sur les séries hypergéométriques de deux variables et sur des équations différentielles linéaires aux dérivées partielles. Comptes rendus hebdomadaires des séances de l'Académie des sciences. 1880, 90: 296–298 and 731–735. JFM 12.0296.01 (法语). (see also "Sur la série F3(α,α',β,β',γ; x,y)" in C. R. Acad. Sci. 90, pp. 977–980)
- Appell, Paul. Sur les fonctions hypergéométriques de deux variables. Journal de Mathématiques Pures et Appliquées. (3ème série). 1882, 8: 173–216 [2015-04-04]. (原始内容存档于2013-04-12) (法语).
- Appell, Paul; Kampé de Fériet, Joseph. Fonctions hypergéométriques et hypersphériques; Polynômes d'Hermite. Paris: Gauthier–Villars. 1926. JFM 52.0361.13 (法语). (see p. 14)
- Askey, R. A.; Daalhuis, Adri B. Olde, 阿佩尔函数, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248
- Bateman, H.; Erdélyi, A. Higher Transcendental Functions, Vol. I (PDF). New York: McGraw–Hill. 1953 [2015-04-04]. (原始内容存档 (PDF)于2011-08-11). (see p. 224)
- Gradshteyn, Izrail' Solomonovich; Ryzhik, Iosif Moiseevich. Tablitsy integralov, summ, ryadov i proizvedeniy [Tables of integrals, sums, series and products] 5th. Moscow: Nauka. 1971 (俄语). (see Chapter 9.18)
- Humbert, Pierre. Sur les fonctions hypercylindriques. Comptes rendus hebdomadaires des séances de l'Académie des sciences. 1920, 171: 490–492. JFM 47.0348.01 (法语).
- Lauricella, Giuseppe. Sulle funzioni ipergeometriche a più variabili. Rendiconti del Circolo Matematico di Palermo. 1893, 7: 111–158. JFM 25.0756.01. doi:10.1007/BF03012437 (意大利语).
- Picard, Émile. Sur une extension aux fonctions de deux variables du problème de Riemann relativ aux fonctions hypergéométriques. Annales scientifiques de l'École Normale Supérieure. (2ème série). 1881, 10: 305–322 [2015-04-04]. JFM 13.0389.01. (原始内容存档于2015-01-21) (法语). (see also C. R. Acad. Sci. 90 (1880), pp. 1119–1121 and 1267–1269)
- Slater, Lucy Joan. Generalized hypergeometric functions. Cambridge, UK: Cambridge University Press. 1966. ISBN 0-521-06483-X. MR 0201688. (there is a 2008 paperback with ISBN 978-0-521-09061-2)