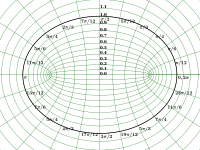
椭圆柱坐标系(英语:Elliptic cylindrical coordinates)是一种三维正交坐标系 。往 z-轴方向延伸二维的椭圆坐标系,则可得到椭圆柱坐标系;其坐标曲面是共焦的椭圆柱面与双曲柱面。椭圆柱坐标系的两个焦点  与
与  的直角坐标,分别设定为
的直角坐标,分别设定为  与
与  ,都处于直角坐标系的 x-轴。
,都处于直角坐标系的 x-轴。
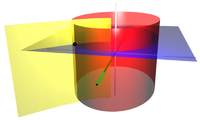
椭圆柱坐标系的几个坐标曲面。红色的椭圆柱面的

。蓝色的薄平面的

。z-轴是垂直的,以白色表示。 x-轴以绿色表示。三个曲面相交于点 P (以黑色的圆球表示),直角坐标大约为

。包含于 xy-平面的椭圆与双曲线的两个焦点的直角坐标为

。
基本定义
椭圆柱坐标 最常见的定义是
- 、
- 、
- ;
其中,实数 ,实数 ,弧度 ,坐标 z 是实数。
的等值曲线形成了椭圆,而 的等值曲线则形成了双曲线:
- 、
- 。
标度因子
椭圆柱坐标 与 的标度因子相等:
- 、
- 。
所以,无穷小体积元素等于
- 。
拉普拉斯算子是
- 。
其它微分算子,例如 与 ,都可以用椭圆柱坐标表达,只需要将标度因子代入正交坐标条目内对应的一般公式。
第二种定义
有时候,会用到另外一种椭圆柱坐标系 ,其中, , 。同样地, 的等值曲线是椭圆,而 的等值曲线是双曲线。在这里, 必须属于区间 ,而 必须大于或等于 。
用椭圆柱坐标系,任何在 xy-平面上的点 ,其与两个焦点的距离 , 有一个很简单的关系(回想两个焦点 与 的坐标分别为 与 ):
- 、
- 。
因此,
- 、
- 。
第二种椭圆柱坐标有一个缺点,那就是它与直角坐标并不保持一一对应关系:
- ,
- 。
第二种标度因子
第二种椭圆柱坐标 的标度因子是
- 、
- 、
- 。
所以,无穷小体积元素等于
- 。
拉普拉斯算子是
- 。
其它微分算子,例如 与 ,都可以用第二种椭圆柱坐标表达,只需要将第二种标度因子代入正交坐标条目内对应的一般公式。
应用
椭圆柱坐标最经典的用途是在解析像拉普拉斯方程或亥姆霍兹方程这类的偏微分方程式。在这些方程式里,椭圆柱坐标允许分离变数法的使用。举一个典型的例题,有一块宽度为 的平板导体,请问其周围的电场为什么?应用椭圆柱坐标,我们可以有条不紊地分析这例题。
三维的波方程,假若用椭圆柱坐标来表达,则可以用分离变数法解析,形成了马蒂厄微分方程 (Mathieu differential equation) 。
参阅
参考文献
- Philip M. Morse, Herman Feshbach. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 657. )
- Henry Margenau, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 182–183.
- Korn GA. Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 179.
- Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 97.
- Moon P, Spencer DE. Elliptic-Cylinder Coordinates (η, ψ, z). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 17–20 (Table 1.03). ISBN 978-0387184302.