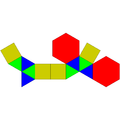
对二侧锥六角柱
在几何学中,对二侧锥六角柱是一种凸十四面体,形如其名地,其可以透过在六角柱“相对”两侧的侧面上各加上一个四角锥来建构,是一种二侧锥六角柱,也是约翰逊多面体之一,编号J55。约翰逊多面体是凸多面体,面皆由正多边形组成但不属于均匀多面体,共有92种。这些立体最早在1966年由诺曼·约翰逊(Norman Johnson)命名并给予描述[1]。
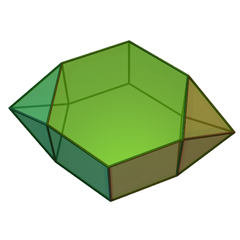 | ||
| 类别 | 约翰逊多面体 J54 - J55 - J56 | |
|---|---|---|
| 对偶多面体 | - | |
| 识别 | ||
| 鲍尔斯缩写 | pabauhip | |
| 性质 | ||
| 面 | 14 | |
| 边 | 26 | |
| 顶点 | 14 | |
| 欧拉特征数 | F=14, E=26, V=14 (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 8个正三角形 4个正方形 2个六边形 | |
| 顶点的种类 | 4个(42.6) 2个(34) 8个(32.4.6) | |
| 对称性 | ||
| 对称群 | D2h | |
| 特性 | ||
| convex | ||
| 图像 | ||
| ||
性质
对二侧锥六角柱可以视为由2个正四角锥(J1)和一个六角柱组合而成的立体,因此其面数、边数和顶点数会与同样是由2个四角锥和1个六角柱组合而成的二侧锥六角柱相同,这些立体有邻二侧锥六角柱和间二侧锥六角柱,它们都有14个面、26条边和14个顶点。在其14个面中,有8个正三角形面、4个正方形面和2个正六边形面。[2]
对二侧锥六角柱的14个顶点可以分成三种,一种是4个三角形的公共顶点,位于侧锥上,共2个;一种是2个三角形、1个正方形和1个六边形的公共顶点,位于侧锥和顶面的交界处,共8个;还有一种是2个正方形和1个六边形的公共顶点,位于原始六角柱底面和侧面的交界,共4个。[3]
二面角
对二侧锥六角柱一共有五种二面角,分别是六角柱两侧面的二面角、六角柱侧面与顶面的二面角、六角柱侧面与侧锥侧面的二面角、六角柱顶面与侧锥侧面的二面角和侧锥侧面的二面角。
其中,六角柱两侧面的二面角为120度;六角柱侧面与顶面的二面角为直角,90度;[4]六角柱侧面与侧锥侧面的二面角为六角柱两侧面的二面角与侧锥底角的和,其中六角柱两侧面的二面角为负二分之一的反余弦值、侧锥(正四角锥)的底角为三平方根的倒数之反余弦值[5],所以六角柱侧面与侧锥侧面的二面角为:
这个角度非常接近平角(180度),也因此,底面边数比6还多的侧锥柱体无法以凸多面体的形式存在(角度超过平角)。
六角柱顶面与侧锥侧面的二面角为:
侧锥侧面的二面角为负三分之一的反余弦值:[5]
体积与表面积
棱长为a的对二侧锥六角柱的表面积(A)和体积(V)为:
顶点坐标
对于一个边长为2且几何中心位于原点的,其顶点坐标为:[2]
相关多面体
同样是由2个四角锥和1个六角柱组合而成的二侧锥六角柱有邻二侧锥六角柱和间二侧锥六角柱。
参考文献
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- ^ 2.0 2.1 The Parabiaugmented Hexagonal Prism. qfbox.info. [2022-09-08]. (原始内容存档于2023-01-15).
- ^ Richard Klitzing. parabiaugmented hexagonal prism, pabauhip. bendwavy.org. [2023-01-15]. (原始内容存档于2023-01-15).
- ^ David I. McCooey. Simplest Canonical Polyhedra of Each Symmetry Type: Simplest Canonical Polyhedron with D6h Symmetry - Hexagonal Prism. [2023-01-15]. (原始内容存档于2023-01-15).
- ^ 5.0 5.1 Richard Klitzing. tetragonal pyramid, squippy. bendwavy.org. [2023-01-15]. (原始内容存档于2023-01-15).
- ^ David I. McCooey. Johnson Solids: Parabiaugmented Hexagonal Prism. [2023-01-15]. (原始内容存档于2023-01-15).
参见
- 间二侧锥六角柱
- 二侧锥六角柱