双心多边形
在几何学中,双心多边形是指同时存在内切圆和外接圆的多边形,换句话说即存在一个圆,能使该多边形的每条边与之相切;也存在另一个圆,能使该多边形的顶点皆落在该圆上。
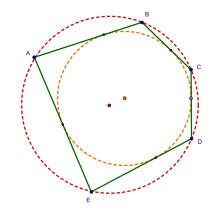
一个双心五边形,同时也属于圆内接五边形和圆外切五边形
双心多边形是一个自身对偶多边形,即其对偶多边形为自己本身,且同时属于圆内接多边形和圆外切多边形。所有三角形和任意边数的正多边形都是双心多边形。另一方面,具有边长不相等的矩形不是双心多边形,因为没有圆可以与所有四个边相切。
双心三角形
所有三角形都同时拥有内切圆和外切圆,因此所有三角形皆为双心多边形[1]。 在任意三角形中,皆可以找到内切圆半径r和外切圆半径R,且它们存在下列等式:
其中,x表示内切圆圆心和外切圆圆心的距离,即内心和外心的距离[2]。这个等式可以视为欧拉三角形公式的其中一个版本。
双心四边形
在所有四边形中,并非所有四边形都可以同时拥有内切圆和外接圆,换句话说并非所有四边形都是双心多边形,而同时拥有内切圆与外接圆的四边形称为双心四边形。
给定2个圆,其中一个圆位于另一个圆内时,假设大圆半径为R、小圆半径为r,若当中存在一个凸四边形,满足每条边与小圆相切、且顶点皆位于大圆上时,则其满足下列式子,反之亦然。[3][4][5]
边数超过4的双心多边形
令外接圆圆心为R、内切圆圆心为r、内心与外心距离为x、n为多边形的边数,更复杂的双心多边形通式为[8]:
其中 、 。
参见
参考文献
- ^ Gorini, Catherine A., The Facts on File Geometry Handbook, Infobase Publishing: 17, 2009 [2018-12-22], ISBN 9780816073894, (原始内容存档于2016-12-23).
- ^ 2.0 2.1 Reiman, István, International Mathematical Olympiad: 1976-1990, Anthem Press: 170–171, 2005, ISBN 9781843312000.
- ^ Dörrie, Heinrich. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover. 1965: 188–193. ISBN 978-0-486-61348-2.
- ^ Yiu, Paul, Euclidean Geometry, [1][永久失效链接], 1998, pp. 158-164.
- ^ Salazar, Juan Carlos, Fuss's Theorem, Mathematical Gazette, 2006,, 90 (July): 306–307.
- ^ Davison, Charles, Subjects for mathematical essays, Macmillan and co., limited: 98, 1915 [2018-12-28], (原始内容存档于2016-12-23).
- ^ Dörrie, Heinrich, 100 Great Problems of Elementary Mathematics: Their History and Solution, Courier Dover Publications: 192, 1965 [2018-12-28], ISBN 9780486613482, (原始内容存档于2014-06-17).
- ^ Weisstein, Eric W. "Poncelet's Porism." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PonceletsPorism.html (页面存档备份,存于互联网档案馆)
外部链接
- 埃里克·韦斯坦因. Bicentric polygon. MathWorld.