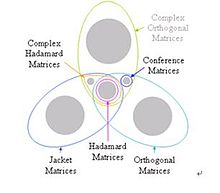
Jacket矩阵

在数学上，一个夹克矩阵为一个n阶的方阵 ${\displaystyle A=(a_{ij})}$ ，内部元素为非0，实数或者是负数的有限值，同时满足下列式子

${\displaystyle \ AB=BA=I_{n}}$ 

其中I_n 代表的是单位矩阵，而 ${\displaystyle \ B={1 \over n}(a_{ij}^{-1})^{T}}$  其中T代表的是转置矩阵的意思。

换句话说，夹克矩阵的反矩阵就是根据其元素或者是其分割的矩阵来决定，基本上反矩阵从其元素倒数再将其做转置可得。

根据以上的定义，整个式子可以表达成如右图所示。

而整个夹克矩阵其实就是阿达马矩阵(Hadamard matrix)的一般式，同时也是对角线block-wise反矩阵。

然而为什么我们会称其为夹克矩阵呢？就如同可正反面穿的夹克一样，在夹克矩阵中，至少有两个地方的元素可被其倒数给取代， 而透过转制这些元素将会被改变其位置。 以下提供一个例子作为参考：

${\displaystyle {\boldsymbol {A}}={\begin{bmatrix}a&{\sqrt {ac}}\\{\sqrt {ac}}&-c\end{bmatrix}}}$ 

此时我们可以将其元素做倒数再转置即可得其反矩阵为:

${\displaystyle {\boldsymbol {A}}^{-1}={\begin{bmatrix}{1 \over a}&{1 \over {\sqrt {ac}}}\\{1 \over {\sqrt {ac}}}&{1 \over -c}\end{bmatrix}}}$ 

可以发现此矩阵满足一开始的定义，此为一个夹克矩阵，然而若我们把a=c=1给代入，将会发现此即为一阿达马的2X2矩阵。

夹克矩阵本身就是阿达马矩阵的一般式，阿达马矩阵为夹克矩阵的特例。

由于整个Jacket matrix基本上就是阿达马矩阵以及中心加权阿达马矩阵的一般式，在这我们先介绍什么是中心加权阿达马矩阵，

基本上跟阿达马矩阵相同，其只需要实数的运算，跟阿达马矩阵比起来，其更注重信号的中频空间频率，

基本上透过中心加权阿达马矩阵的分解我们可以发展出一个WHT的快速算法。

而矩阵的分解主要是透过克罗内客基(Kronecker product)相乘基本的中心加权阿达马矩阵以及其前一个阶级的中心加权阿达马矩阵。

而最低阶的中心加权阿达马矩阵为一个4*4的方形矩阵，其定义如下:

${\displaystyle [WH]_{4}=\left[{\begin{array}{rrrr}1&1&1&1\\1&-w&w&-1\\1&w&-w&-1\\1&-1&-1&1\\\end{array}}\right]}$ 

而其反矩阵则如下所式：

${\displaystyle [WH]_{4}^{-1}=\left[{\begin{array}{rrrr}1&1&1&1\\[6pt]1&{-1 \over w}&{1 \over w}&-1\\[6pt]1&{1 \over w}&{-1 \over w}&-1\\[6pt]1&-1&-1&1\\[6pt]\end{array}}\right]}$ 

当w=1 的时候，此时则为一个阿达马矩阵，而如果当w=2代入的时候，其为一个中心加权阿达马矩阵。

而如果我们想去计算更高阶的中心加权阿达马矩阵的话，透过阿达马矩阵的帮助，我们可以用一个递回的方式来得到答案，如下式所表示:

${\displaystyle [WH]_{N}=[WH]_{N \over 2}X[H]_{2}}$ 

而这里的相乘 X 代表的是克罗内克积(Kronecker product)，而[H]₂代表的则是最低阶的阿达马矩阵

${\displaystyle {\boldsymbol {H_{2}}}={\begin{bmatrix}1&1\\1&-1\end{bmatrix}}}$ 

例如当我们想去计算[WH]₈则可以如下去计算而得:

${\displaystyle [WH]_{8}=[WH]_{4}X[H]_{2}}$ 

${\displaystyle =\left[{\begin{array}{rrrr}1&1&1&1\\1&-2&2&-1\\1&2&-2&-1\\1&-1&-1&1\\\end{array}}\right]X{\boldsymbol {\begin{bmatrix}1&1\\1&-1\end{bmatrix}}}}$ 

${\displaystyle =\left[{\begin{array}{rrrrrrrr}1&1&1&1&1&1&1&1\\1&-1&1&-1&1&-1&1&-1\\1&1&-2&-2&2&2&-1&-1\\1&-1&-2&2&2&-2&-1&1\\1&1&2&2&-2&-2&-1&-1\\1&-1&2&-2&-2&2&-1&-1\\1&1&-1&-1&-1&-1&1&1\\1&-1&-1&1&-1&1&1&-1\\\end{array}}\right]}$ 

而根据以上我们可以发现，中心加权阿达马矩阵及其反矩阵恰好满足夹克矩阵的定义，于是任何的中心加权阿达马矩阵都是夹克矩阵的一种。

为了要去使用这个快速算法，首先我们先定义一个加权系数矩阵[RC]_N为下式:

${\displaystyle [RC]_{N}=[H]_{N}[WH]_{N}}$ 

而整个[RC]_N本身为一个稀疏矩阵，根据下式我们可以发现[RC]_N可以低阶的[RC]_(N/2)来表示:

${\displaystyle [RC]_{N}=([H]_{N \over 2}X[H]_{2})([WH]_{N \over 2}X[H]_{2})}$ 

        ${\displaystyle =([H]_{N \over 2}[WH]_{N \over 2})X([H]_{2}[H]_{2})}$ 
            
        ${\displaystyle =[RC]_{N \over 2}X2[I]_{2}}$ 

这边的X同理代表的为克罗内克基(Kronecker product)，而[I]₂代表的为2X2的单位矩阵。 根据阿达马矩阵的特性

${\displaystyle [H]_{N}^{-1}={1 \over N}[H]_{N}}$ 

我们可以将中心加权阿达马矩阵表示如下：

${\displaystyle [WH]_{N}={1 \over N}[H]_{N}[RC]_{N}}$ 

${\displaystyle [WH]_{N}^{-1}=N[H]_{N}^{-1}[RC]_{N}^{-1}}$ 

故同样以N=8为例子，在计算[WH]₈时则可如下表示:

${\displaystyle [WH]_{8}={1 \over 8}[H]_{8}[RC]_{8}}$ 

        ${\displaystyle =({1 \over 8}[H]_{4}X[H]_{2})([RC]_{4}X2[I]_{2})}$ 

        ${\displaystyle ={1 \over 8}([H]_{4}[RC]_{4})X2[H]_{2})}$ 

于是我们可以借由低级数的阿达马矩阵和中心加权阿达马矩阵来快速地计算高阶的阿达马矩阵。

1. 任意一个夹克矩阵其必定为对称矩阵，即转置后的结果与转置前相等。

2.对任意一个整数n来说，必定存在一个级数为n的夹克矩阵。

3.如果A矩阵为一个复数的阿达马矩阵，其必定为一个夹克矩阵。

4.若一个矩阵A为一夹克矩阵，同时其内部元素A_ij的绝对值皆为1，则此矩阵也是一个复数的阿达马矩阵。

若里面的内部元素A_ij为实数，且任一元素平方的值皆为1，则此矩阵也是一个阿达马矩阵。

5.若A为一个夹克矩阵，则其共厄矩阵 A^* 其转置矩阵A^T 其反矩阵A^-1也都会是夹克矩阵。

6.若A为一个夹克矩阵，而D跟E为对角方阵，则DAE也会是一个夹克矩阵。

对任意一个级数为2的夹克矩阵，其型式必定为下面所示之矩阵:

${\displaystyle {\boldsymbol {J_{2}}}={\begin{bmatrix}1&1\\1&-1\end{bmatrix}}}$ 

对任意一个级数为3的夹克矩阵，其型式为下面所示之矩阵:

${\displaystyle [J]_{3}=\left[{\begin{array}{rrr}1&1&1\\1&w&w^{2}\\1&w^{2}&w\\\end{array}}\right]}$ 

对任意一个级数为4夹克矩阵，其型式必定为下面所示之矩阵:

${\displaystyle [J]_{4}=\left[{\begin{array}{rrrr}1&1&1&1\\1&-w&w&-1\\1&w&-w&-1\\1&-1&-1&1\\\end{array}}\right]}$ 

Moon Ho Lee,The Center Weighted Hadamard Transform, IEEE Transactions on Circuits Syst. Vol. 36, No. 9, PP. 1247–1249, Sept.1989.

K.J. Horadam, Hadamard Matrices and Their Applications, Princeton University Press, UK, Chapter 4.5.1: The jacket matrix construction, PP. 85–91, 2007.

Moon Ho Lee, Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing,LAP LAMBERT Publishing, Germany,Nov. 2012

Moon Ho Lee, On Jacket Matrices Based on Weighted Hadamard Matrices. JKEES 2007-1-04

• Technical report: Linear-fractional Function, Elliptic Curves, and Parameterized Jacket Matrices
• Jacket Matrix and Its Fast Algorithms for Cooperative Wireless Signal Processing
• Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing （页面存档备份，存于互联网档案馆）
• On Jacket Matrices Based on Weighted Hadamard Matrices（页面存档备份，存于互联网档案馆）