斯托克斯数

  此条目介绍的是有关悬浮在流场上物体的无量纲。关于描述脉动流频率以及黏滞效应之间的关系的无量纲，请见“沃默斯利数”。

斯托克斯数（Stk）得名自乔治·斯托克斯，是流体力学的无量纲，描述悬浮在流场上物体的行为。斯托克斯数定义为物体（或液滴）特征时间和流场特征时间的比值，也就是

从实验中得到，球的阻力系数C_d和雷诺数之间的关系。实线表示是表面光滑的球，而虚线是表面粗糙的球。线上的数字表示不同的流型及其对流型的影响：
•2：附着流（斯托克斯流）以及稳定的分离流
•3：分离的不稳定流，有边界层分离的上游有层流的边界层，下游会产生卡门涡街
•4：分离的不稳定流，有边界层分离的上游有层流的边界层，下游会有浑沌的紊流船波
•5：后临界分离流，有紊流边界层

${\displaystyle \mathrm {Stk} ={\frac {t_{0}\,u_{0}}{l_{0}}}}$

其中

${\displaystyle t_{0}}$为物体的驰豫时间（因为阻力造成物体速度指数衰减的时间常数）

${\displaystyle u_{0}}$是流场在远离物体处的速度

${\displaystyle l_{0}}$为物体的特征尺寸（多半是直径）

若一物体的斯托克斯数低，表示其可以顺着流场的流线（完全移流），而斯托克斯数高时，表示受惯性的影响大，会顺着原来轨迹继续前进。

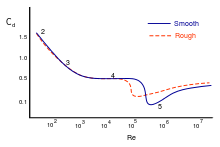
在斯托克斯流中，也就是雷诺数够低的流体，其阻力系数和雷诺数成反比，物体的特性时间可以定义为

${\displaystyle t_{0}={\frac {\rho _{d}d_{d}^{2}}{18\mu _{g}}}}$

其中

${\displaystyle \rho _{d}}$为物体密度

${\displaystyle d_{d}}$为物体直径

${\displaystyle \mu _{g}}$为气体的黏度^[1]

在实验流体力学中，粒子图像测速仪（英语：Particle image velocimetry）会将很小的粒子放在紊流中，再用光观察流体运动的速度及方向（也称为流体的速度场），斯托克斯数用来可以粒子图像测速仪中，流体示踪剂的保真性。若要有足够的示踪准确性，粒子的反应时间需要比流场的最小时间刻度要快。斯托克斯数小表示示踪准确性较高，若${\displaystyle \mathrm {Stk} \gg 1}$，在流场快速减速时，粒子会和流场分离。若${\displaystyle \mathrm {Stk} \ll 1}$，粒子会跟着流场。若${\displaystyle \mathrm {Stk} \ll 0.1}$，示踪准确性误差会小于1%^[2]。