击中时

设${\displaystyle T}$ 是一个有序的指标集，比如说是自然数的集合${\displaystyle \mathbb {N} }$ 、非负实数集${\displaystyle \mathbb {R} ^{+}=[0,+\infty )}$ 或者是这两者的子集。${\displaystyle T}$ 中的一个元素${\displaystyle t\in T}$ 可以被认为是一种记录时间的方式（离散或连续型）。给定一个概率空间${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$ ，一个可测状态空间${\displaystyle S}$ ，设${\displaystyle X:\,\,\Omega \times T\rightarrow S=\left(X_{t}\right)_{t\in T}}$ 为一个随机过程，并设${\displaystyle A}$ 为${\displaystyle S}$ 中的一个可测子集。那么，随机过程${\displaystyle \left(X_{t}\right)_{t\in T}}$ 首次接触子集${\displaystyle A}$ 的击中时定义为以下的随机变量^[1]:155：

${\displaystyle \tau _{A}\Omega \longrightarrow {\overline {T}}}$ 

${\displaystyle \tau _{A}(\omega ):=\,\,\inf\{t\in T\,|\,X_{t}(\omega )\in A\}.}$ 

同样，可以定义${\displaystyle \left(X_{t}\right)_{t\in T}}$ 首次离开子集${\displaystyle A}$ 的离时：

${\displaystyle \epsilon _{A}(\omega ):=\,\,\inf\{t\in T\,|\,X_{t}(\omega )\notin A\}=\,\inf\{t\in T\,|\,X_{t}(\omega )\in A^{c}\}=\tau _{A^{c}}.}$ 

可以看出离时实际上也是击中时的一种，表示首次接触到要研究的子集的补集的时间。很多时候，离时也会记为${\displaystyle \tau _{A}}$ ，和击中时一样。

另外一种击中时是 ${\displaystyle \left(X_{t}\right)_{t\in T}}$ 后首次回到出发点${\displaystyle \{X_{0}(\omega )\}}$ 的击中时，称为回时或首次回归时间：

${\displaystyle \tau _{0}(\omega ):=\,\,\inf\{t\in T\,|\,X_{t}(\omega )=X_{0}(\omega )\}.}$ 

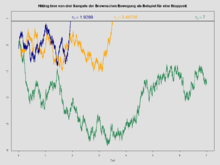
• 设${\displaystyle \left(W_{t}\right)_{t\in \mathbb {R} ^{+}}}$ 为${\displaystyle \mathbb {R} }$ 上标准的布朗运动过程，则对于任意（实数的）波莱尔可测子集${\displaystyle A}$ ，都可以定义首次接触${\displaystyle A}$ 的击中时${\displaystyle \tau _{A}^{W}}$ ，并且可以证明这样定义的击中时${\displaystyle \tau _{A}^{W}}$ 都是停时。

• 如果定义标准布朗运动${\displaystyle \left(W_{t}\right)_{t\in \mathbb {R} ^{+}}}$ 首次离开区间${\displaystyle A_{r}=(-r,r)}$ 的离时为${\displaystyle \epsilon _{r}^{W}=\tau _{A_{r}^{c}}^{W}}$ ，那么这个离时也是停时，它的数学期望是：${\displaystyle \mathbb {E} (\epsilon _{r}^{W})=r^{2}}$ ，方差是${\displaystyle \operatorname {Var} (\epsilon _{r}^{W})={\frac {2}{3}}r^{4}.}$ 

对于给定的概率空间，随机过程首次进入状态空间中的一个可测子集${\displaystyle F}$ 的击中时也称为${\displaystyle F}$ 的首发时间（début）。首发定理说明，如果随机过程是循序可测的，那么可测子集的首发时间一定是停时。循序可测过程包括所有的左连续适应过程和右连续适应过程。首发定理的证明用到了解析集的性质。首发定理需要概率空间是完全概率空间。

首发定理的逆定理指出，所有定义在某个实数时间轴的滤波上的停时，都能表示为某个状态空间子集的击中时。特别地，存在一个适应的不增随机过程，其路径几乎总是左极限右连续，并且取值为0或1，使得子集${\displaystyle \{0\}}$ 的击中时就是对应的停时。

• 停时

• Fischer, Tom. On simple representations of stopping times and stopping time sigma-algebras. Statistics and Probability Letters. 2013, 83 (1): 345–349. doi:10.1016/j.spl.2012.09.024. 

• Øksendal, Bernt K. Stochastic Differential Equations: An Introduction with Applications Sixth edition. Berlin: Springer. 2003. ISBN 3-540-04758-1.  引文格式1维护：冗余文本 (link)