在微积分学中,上极限和下极限(英语:Limit superior and limit inferior)是指数列极限的上极限和下极限,可以大致想像为数列极限的上下界。举例来说,数列  的上极限为 1,下极限为 -1。
函数的上极限和下极限可以用类似方式考虑。[注 1]。集合的上极限和下极限分别是这个集合的极限点的上确界和下确界。
的上极限为 1,下极限为 -1。
函数的上极限和下极限可以用类似方式考虑。[注 1]。集合的上极限和下极限分别是这个集合的极限点的上确界和下确界。
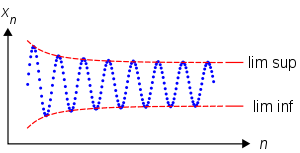
上极限和下极限的示意图。数列
xn 为蓝色。两个红色虚线曲线逼近数列
xn 的上极限和下极限。数列的上下极限相等当且仅当此数列
收敛定义
序列 的上极限定义是
- ;
或者
- 。
同样的,序列 的下极限定义是
- ;
或者
- 。
这些定义在任意的偏序集都适用,只需要上确界和下确界存在。
在完全格里,上确界和下确界总是存在,所以其中的序列一定有上极限和下极限。
每当 和 都存在,那么
- 。
上极限和下极限也记为 和 。
实数数列
实数集 R 的数列对微积分很重要。R 不是完备格,但可以加入正负无穷以得到完备全序集 ,形成完备格。那么在 中数列
收敛当且仅当 ,而这时 等于上面的共同值。[注 2]
若实数数列 的上极限为实数[注 3],那么上极限是最小的实数 a,使得对任意小的正实数 ,都存在足够大的正整数 N,使得对所有 ,都有 。换言之,对任何大于上极限的实数,都存在 N 使得这实数是数列 的上界。
若实数数列 的下极限为实数,那么下极限是最大的实数 b,使得对任意小的正实数 ,都存在足够大的正整数 N,使得对所有 ,都有 。换言之,对任何小于下极限的实数,都存在 N 使得这实数是数列 的下界。
设 是整数数列。若其上极限为实数 a,由于 也符合上述条件,故此 a 必是整数。[注 4]在条件中取 ,得出 a 是最小的实数,使得存在正整数 N,对所有 ,都有 。因此 a 是最大的整数,使得有无限个 。同样地,若其下极限为实数 b,则 b 是最小的整数,使得有无限个 。
若 和
,那么区间 不一定包含任何的 ,但是轻微扩大了的 [I-ε,S+ε]
对任意小的ε > 0都会包含除了有限项外所有的 xn。区间 [I, S] 是适合这个性质的最小闭区间。
例子
- 设 ,则 , 。闭区间[-1, 1]中不包含任何 。
- 考虑数列 。应用π的无理数性质,可以证明 和 。[注 5]
-
- 其中 是第 个素数。[注 6]
集的序列
集合X的幂集P(X)是完备格。对于P(X)中的序列,也就是X的子集的序列,其上下极限也有用处。
若 是这样的序列,那么X的元素a属于 ,当且仅当存在自然数 使得对于所有 ,a在 里。元素a属于 ,当且仅当对所有自然数 ,都存在一个指数 使得a在 里。换句话说, 包含了所有这样的元素,其中的每一个,都有无限多个n,使得它在集合 里;而 包含了所有这样的元素,其中的每一个,都有除了有限多个外的所有n,使得它在 里。
以集合论的标准语言来说,一个集合序列的下确界是这些集合的可数交,也就是包含在所有集合里的最大集合:
- 。
令 为自 起的集合的下确界。那么序列 非递减,因为 。所以,第1至n个下确界的并集就是第n个下确界。下极限就是这序列的极限:
- 。
上极限可以相反方式定义。一个集合序列的上确界是包含这些集合的最小集合,也就是它们的可数并:
- 。
上极限是这个非递增的上确界序列的可数交(其中每个上确界都包含在前一个里面)。
- 。
例子或应用可见波莱尔-坎泰利引理,柯西-阿达马公式(Cauchy-Hadamard Formula)。
注释
引用
- Amann, H.; Escher, Joachim. Analysis. Basel; Boston: Birkhäuser. 2005. ISBN 0817671536.
- González, Mario O. Classical complex analysis. New York: M. Dekker. 1991. ISBN 0824784154.

