关于同名角度单位,请见“
梯度 (角) ”。
在向量微积分 中,梯度 (英语:gradient )是一种关于多元导数 的概括[1] 函数 的导数是标量值函数 ,而多元函数 的梯度是向量值函数 。多元 可微函数
f
{\displaystyle f}
P
{\displaystyle P}
f
{\displaystyle f}
P
{\displaystyle P}
偏导数 为分量的向量 [2]
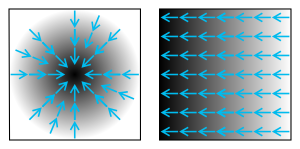
上面两个图中,标量场的值用
灰度 表示,越暗表示越大的数值,而其相应的梯度用蓝色箭头表示。
就像一元函数的导数表示这个函数图形 的切线 的斜率 [3]
P
{\displaystyle P}
方向 是这个函数在
P
{\displaystyle P}
量 是在这个方向上的增长率[4]
梯度向量中的幅值和方向是与坐标的选择无关的独立量[5]
在欧几里德空间 或更一般的流形 之间的多元可微映射 的向量值函数的梯度推广是雅可比矩阵 [6] 巴拿赫空间 之间的函数的进一步推广是弗雷歇导数 。
梯度的解释
将2D函数
f (x , y ) = xe −(x 2 + y 2 ) 的梯度绘制为蓝色箭头,还绘制了这个函数的伪色图。
假设有一个房间,房间内所有点的温度由一个标量场
ϕ
{\displaystyle \phi }
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
ϕ
(
x
,
y
,
z
)
{\displaystyle \phi (x,y,z)}
考虑一座高度在
(
x
,
y
)
{\displaystyle (x,y)}
H
(
x
,
y
)
{\displaystyle H(x,y)}
H
{\displaystyle H}
坡度 (或者说斜度 )最陡的方向。梯度的大小告诉我们坡度到底有多陡。
梯度也可以告诉我们一个数量在不是最快变化方向的其他方向的变化速度。再次考虑山坡的例子。可以有条直接上山的路其坡度是最大的,则其坡度是梯度的大小。也可以有一条和上坡方向成一个角度的路,例如投影在水平面上的夹角为60°。则,若最陡的坡度是40%,这条路的坡度小一点,是20%,也就是40%乘以60°的余弦。
这个现象可以如下数学的表示。山的高度函数
H
{\displaystyle H}
点积 一个单位向量 给出表面在该向量的方向上的斜率。这称为方向导数 。
定义
将函数
f (x ,y ) = −(cos2 x + cos2 y )2 的梯度描绘为在底面上投影的
向量场 。
标量函数
f
:
R
n
↦
R
{\displaystyle f\colon \mathbb {R} ^{n}\mapsto \mathbb {R} }
∇
f
{\displaystyle \nabla f}
grad
f
{\displaystyle \operatorname {grad} f}
∇
{\displaystyle \nabla }
nabla )表示向量微分算子 。
函数
f
{\displaystyle f}
∇
f
{\displaystyle \nabla f}
v
(
∇
f
(
x
)
)
⋅
v
=
D
v
f
(
x
)
{\displaystyle {\big (}\nabla f(x){\big )}\cdot \mathbf {v} =D_{\mathbf {v} }f(x)}
直角坐标系
∇
f
{\displaystyle \nabla f}
直角坐标系 中表示为
∇
f
=
(
∂
f
∂
x
,
∂
f
∂
y
,
∂
f
∂
z
)
=
∂
f
∂
x
i
+
∂
f
∂
y
j
+
∂
f
∂
z
k
{\displaystyle \nabla f={\begin{pmatrix}{\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}},{\frac {\partial f}{\partial z}}\end{pmatrix}}={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k} }
i j k x y z 参看偏导数 和向量 。 )
虽然使用坐标表达,但结果是在正交变换 下不变,从几何的观点来看,这是应该的。
举例来讲,函数
f
(
x
,
y
,
z
)
=
2
x
+
3
y
2
−
sin
(
z
)
{\displaystyle f(x,y,z)=2x+3y^{2}-\sin(z)}
∇
f
=
(
2
,
6
y
,
−
cos
(
z
)
)
=
2
i
+
6
y
j
−
cos
(
z
)
k
{\displaystyle \nabla f={\begin{pmatrix}{2},{6y},{-\cos(z)}\end{pmatrix}}=2\mathbf {i} +6y\mathbf {j} -\cos(z)\mathbf {k} }
圆柱坐标系 在圆柱坐标系 中,
f
{\displaystyle f}
[7]
∇
f
(
ρ
,
φ
,
z
)
=
∂
f
∂
ρ
e
ρ
+
1
ρ
∂
f
∂
φ
e
φ
+
∂
f
∂
z
e
z
{\displaystyle \nabla f(\rho ,\varphi ,z)={\frac {\partial f}{\partial \rho }}\mathbf {e} _{\rho }+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}\mathbf {e} _{\varphi }+{\frac {\partial f}{\partial z}}\mathbf {e} _{z}}
ρ φ 投影线 与正 x-轴之间的夹角。
z 直角坐标 的
z
{\displaystyle z}
e ρ e φ e z
球坐标系 在球坐标系 中:
∇
f
(
r
,
θ
,
φ
)
=
∂
f
∂
r
e
r
+
1
r
∂
f
∂
θ
e
θ
+
1
r
sin
θ
∂
f
∂
φ
e
φ
{\displaystyle \nabla f(r,\theta ,\varphi )={\frac {\partial f}{\partial r}}\mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}\mathbf {e} _{\theta }+{\frac {1}{r\sin \theta }}{\frac {\partial f}{\partial \varphi }}\mathbf {e} _{\varphi }}
其中θ φ
实值函数相对于向量和矩阵的梯度
相对于n×1向量x 的梯度算子记作
∇
x
{\displaystyle \nabla _{\boldsymbol {x}}}
[8]
∇
x
=
d
e
f
[
∂
∂
x
1
,
∂
∂
x
2
,
⋯
,
∂
∂
x
n
]
T
=
∂
∂
x
{\displaystyle \nabla _{\boldsymbol {x}}{\overset {\underset {\mathrm {def} }{}}{=}}\left[{\frac {\partial }{\partial x_{1}}},{\frac {\partial }{\partial x_{2}}},\cdots ,{\frac {\partial }{\partial x_{n}}}\right]^{T}={\frac {\partial }{\partial {\boldsymbol {x}}}}}
对向量的梯度 以n×1实向量x 为变元的实标量函数f(x )相对于x 的梯度为一n×1列向量x ,定义为
∇
x
f
(
x
)
=
d
e
f
[
∂
f
(
x
)
∂
x
1
,
∂
f
(
x
)
∂
x
2
,
⋯
,
∂
f
(
x
)
∂
x
n
]
T
=
∂
f
(
x
)
∂
x
{\displaystyle \nabla _{\boldsymbol {x}}f({\boldsymbol {x}}){\overset {\underset {\mathrm {def} }{}}{=}}\left[{\frac {\partial f({\boldsymbol {x}})}{\partial x_{1}}},{\frac {\partial f({\boldsymbol {x}})}{\partial x_{2}}},\cdots ,{\frac {\partial f({\boldsymbol {x}})}{\partial x_{n}}}\right]^{T}={\frac {\partial f({\boldsymbol {x}})}{\partial {\boldsymbol {x}}}}}
m维行向量函数
f
(
x
)
=
[
f
1
(
x
)
,
f
2
(
x
)
,
⋯
,
f
m
(
x
)
]
{\displaystyle {\boldsymbol {f}}({\boldsymbol {x}})=[f_{1}({\boldsymbol {x}}),f_{2}({\boldsymbol {x}}),\cdots ,f_{m}({\boldsymbol {x}})]}
x 的梯度为一n×m矩阵,定义为
∇
x
f
(
x
)
=
d
e
f
[
∂
f
1
(
x
)
∂
x
1
∂
f
2
(
x
)
∂
x
1
⋯
∂
f
m
(
x
)
∂
x
1
∂
f
1
(
x
)
∂
x
2
∂
f
2
(
x
)
∂
x
2
⋯
∂
f
m
(
x
)
∂
x
2
⋮
⋮
⋱
⋮
∂
f
1
(
x
)
∂
x
n
∂
f
2
(
x
)
∂
x
n
⋯
∂
f
m
(
x
)
∂
x
n
]
=
∂
f
(
x
)
∂
x
{\displaystyle \nabla _{\boldsymbol {x}}{\boldsymbol {f}}({\boldsymbol {x}}){\overset {\underset {\mathrm {def} }{}}{=}}{\begin{bmatrix}{\frac {\partial f_{1}({\boldsymbol {x}})}{\partial x_{1}}}&{\frac {\partial f_{2}({\boldsymbol {x}})}{\partial x_{1}}}&\cdots &{\frac {\partial f_{m}({\boldsymbol {x}})}{\partial x_{1}}}\\{\frac {\partial f_{1}({\boldsymbol {x}})}{\partial x_{2}}}&{\frac {\partial f_{2}({\boldsymbol {x}})}{\partial x_{2}}}&\cdots &{\frac {\partial f_{m}({\boldsymbol {x}})}{\partial x_{2}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial f_{1}({\boldsymbol {x}})}{\partial x_{n}}}&{\frac {\partial f_{2}({\boldsymbol {x}})}{\partial x_{n}}}&\cdots &{\frac {\partial f_{m}({\boldsymbol {x}})}{\partial x_{n}}}\\\end{bmatrix}}={\frac {\partial {\boldsymbol {f}}({\boldsymbol {x}})}{\partial {\boldsymbol {x}}}}}
对矩阵的梯度 标量函数
f
(
A
)
{\displaystyle f({\boldsymbol {A}})}
A 的梯度为一m×n矩阵,简称梯度矩阵,定义为
∇
A
f
(
A
)
=
d
e
f
[
∂
f
(
A
)
∂
a
11
∂
f
(
A
)
∂
a
12
⋯
∂
f
(
A
)
∂
a
1
n
∂
f
(
A
)
∂
a
21
∂
f
(
A
)
∂
a
22
⋯
∂
f
(
A
)
∂
a
2
n
⋮
⋮
⋱
⋮
∂
f
(
A
)
∂
a
m
1
∂
f
(
A
)
∂
a
m
2
⋯
∂
f
(
A
)
∂
a
m
n
]
=
∂
f
(
A
)
∂
A
{\displaystyle \nabla _{\boldsymbol {A}}f({\boldsymbol {A}}){\overset {\underset {\mathrm {def} }{}}{=}}{\begin{bmatrix}{\frac {\partial f({\boldsymbol {A}})}{\partial a_{11}}}&{\frac {\partial f({\boldsymbol {A}})}{\partial a_{12}}}&\cdots &{\frac {\partial f({\boldsymbol {A}})}{\partial a_{1n}}}\\{\frac {\partial f({\boldsymbol {A}})}{\partial a_{21}}}&{\frac {\partial f({\boldsymbol {A}})}{\partial a_{22}}}&\cdots &{\frac {\partial f({\boldsymbol {A}})}{\partial a_{2n}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial f({\boldsymbol {A}})}{\partial a_{m1}}}&{\frac {\partial f({\boldsymbol {A}})}{\partial a_{m2}}}&\cdots &{\frac {\partial f({\boldsymbol {A}})}{\partial a_{mn}}}\\\end{bmatrix}}={\frac {\partial {\boldsymbol {f}}({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}}
法则 以下法则适用于实标量函数对向量的梯度以及对矩阵的梯度。
线性法则:若
f
(
A
)
{\displaystyle f({\boldsymbol {A}})}
g
(
A
)
{\displaystyle g({\boldsymbol {A}})}
1 和c2 为实常数,则
∂
[
c
1
f
(
A
)
+
c
2
g
(
A
)
]
∂
A
=
c
1
∂
f
(
A
)
∂
A
+
c
2
∂
g
(
A
)
∂
A
{\displaystyle {\frac {\partial [c_{1}f({\boldsymbol {A}})+c_{2}g({\boldsymbol {A}})]}{\partial {\boldsymbol {A}}}}=c_{1}{\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+c_{2}{\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}}
乘积法则:若
f
(
A
)
{\displaystyle f({\boldsymbol {A}})}
g
(
A
)
{\displaystyle g({\boldsymbol {A}})}
h
(
A
)
{\displaystyle h({\boldsymbol {A}})}
∂
f
(
A
)
g
(
A
)
∂
A
=
g
(
A
)
∂
f
(
A
)
∂
A
+
f
(
A
)
∂
g
(
A
)
∂
A
{\displaystyle {\frac {\partial f({\boldsymbol {A}})g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}=g({\boldsymbol {A}}){\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+f({\boldsymbol {A}}){\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}}
∂
f
(
A
)
g
(
A
)
h
(
A
)
∂
A
=
g
(
A
)
h
(
A
)
∂
f
(
A
)
∂
A
+
f
(
A
)
h
(
A
)
∂
g
(
A
)
∂
A
+
f
(
A
)
g
(
A
)
∂
h
(
A
)
∂
A
{\displaystyle {\frac {\partial f({\boldsymbol {A}})g({\boldsymbol {A}})h({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}=g({\boldsymbol {A}})h({\boldsymbol {A}}){\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+f({\boldsymbol {A}})h({\boldsymbol {A}}){\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+f({\boldsymbol {A}})g({\boldsymbol {A}}){\frac {\partial h({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}}
商法则:若
g
(
A
)
≠
0
{\displaystyle g({\boldsymbol {A}})\neq 0}
∂
f
(
A
)
/
g
(
A
)
∂
A
=
1
g
(
A
)
2
[
g
(
A
)
∂
f
(
A
)
∂
A
−
f
(
A
)
∂
g
(
A
)
∂
A
]
{\displaystyle {\frac {\partial f({\boldsymbol {A}})/g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}={\frac {1}{g({\boldsymbol {A}})^{2}}}\left[g({\boldsymbol {A}}){\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}-f({\boldsymbol {A}}){\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}\right]}
链式法则:若A 为m×n矩阵,且
y
=
f
(
A
)
{\displaystyle y=f({\boldsymbol {A}})}
g
(
y
)
{\displaystyle g(y)}
A 和标量y为变元的实标量函数,则
∂
g
(
f
(
A
)
)
∂
A
=
d
g
(
y
)
d
y
∂
f
(
A
)
∂
A
{\displaystyle {\frac {\partial g(f({\boldsymbol {A}}))}{\partial {\boldsymbol {A}}}}={\frac {dg(y)}{dy}}{\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}}
流形上的梯度
一个黎曼流形
M
{\displaystyle M}
f
{\displaystyle f}
∇
f
{\displaystyle \nabla f}
向量场 ,使得对于每个向量
ξ
{\displaystyle \xi }
⟨
∇
f
,
ξ
⟩
:=
ξ
f
{\displaystyle \langle \nabla f,\xi \rangle :=\xi f}
其中
⟨
⋅
,
⋅
⟩
{\displaystyle \langle \cdot ,\cdot \rangle }
M
{\displaystyle M}
内积 (度量)而
ξ
f
(
p
)
,
p
∈
M
{\displaystyle \xi f(p),p\in M}
f
{\displaystyle f}
p
{\displaystyle p}
ξ
(
p
)
{\displaystyle \xi (p)}
方向导数 。换句话说,如果
φ
:
U
⊆
M
↦
R
n
{\displaystyle \varphi :U\subseteq M\mapsto \mathbb {R} ^{n}}
p
{\displaystyle p}
ξ
(
x
)
=
∑
j
a
j
(
x
)
∂
∂
x
j
{\displaystyle \xi (x)=\sum _{j}a_{j}(x){\frac {\partial }{\partial x_{j}}}}
ξ
f
(
p
)
{\displaystyle \xi f(p)}
ξ
(
f
∣
p
)
:=
∑
j
a
j
(
∂
∂
x
j
(
f
∘
φ
−
1
)
∣
φ
(
p
)
)
{\displaystyle \xi (f\mid _{p}):=\sum _{j}a_{j}({\frac {\partial }{\partial x_{j}}}(f\circ \varphi ^{-1})\mid _{\varphi (p)})}
函数的梯度和外微分 相关,因为
ξ
f
=
d
f
(
ξ
)
{\displaystyle \xi f=df(\xi )}
d
f
{\displaystyle df}
∇
f
{\displaystyle \nabla f}
∇
f
{\displaystyle \nabla f}
d
f
(
ξ
)
=
⟨
∇
f
,
ξ
⟩
{\displaystyle df(\xi )=\langle \nabla f,\xi \rangle }
f
{\displaystyle f}
d
f
{\displaystyle df}
{
d
f
}
{\displaystyle \{df\}}
{
∇
f
}
{\displaystyle \{\nabla f\}}
满射 。
由定义可算流形
∇
f
{\displaystyle \nabla f}
∇
f
=
∑
i
k
g
i
k
∂
f
∂
x
k
∂
∂
x
i
{\displaystyle \nabla f=\sum _{ik}g^{ik}{\frac {\partial f}{\partial x^{k}}}{\frac {\partial }{\partial x^{i}}}}
请注意这是流形
d
s
2
=
∑
i
j
g
i
j
d
x
i
d
x
j
{\displaystyle ds^{2}=\sum _{ij}g_{ij}dx^{i}dx^{j}}
R
n
{\displaystyle \mathbb {R} ^{n}}
∑
{\displaystyle \sum }
参看 参考文献
引用
^ Beauregard & Fraleigh (1973 , p. 84)^ Bachman (2007 , p. 76)Beauregard & Fraleigh (1973 , p. 84)Downing (2010 , p. 316)Harper (1976 , p. 15)Kreyszig (1972 , p. 307)McGraw-Hill (2007 , p. 196)Moise (1967 , p. 683)Protter & Morrey, Jr. (1970 , p. 714)Swokowski et al. (1994 , p. 1038)^ Protter & Morrey, Jr. (1970 , pp. 21,88)^ Bachman (2007 , p. 77)Downing (2010 , pp. 316–317)Kreyszig (1972 , p. 309)McGraw-Hill (2007 , p. 196)Moise (1967 , p. 684)Protter & Morrey, Jr. (1970 , p. 715)Swokowski et al. (1994 , pp. 1036,1038–1039)^ Kreyszig (1972 , pp. 308–309)Stoker (1969 , p. 292)^ Beauregard & Fraleigh (1973 , pp. 87,248)Kreyszig (1972 , pp. 333,353,496)^ Schey 1992 ,第139–142页.^ 张贤达 (2004 , p. 258)
来源
书籍 Bachman, David, Advanced Calculus Demystified, New York: McGraw-Hill , 2007, ISBN 0-07-148121-4 Beauregard, Raymond A.; Fraleigh, John B., A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company ISBN 0-395-14017-X Downing, Douglas, Ph.D., Barron's E-Z Calculus, New York: Barron's ISBN 978-0-7641-4461-5 Dubrovin, B. A.; Fomenko, A. T.; Novikov, S. P. Modern Geometry—Methods and Applications: Part I: The Geometry of Surfaces, Transformation Groups, and Fields. Graduate Texts in Mathematics 2nd. Springer. 1991. ISBN 978-0-387-97663-1 Harper, Charlie, Introduction to Mathematical Physics, New Jersey: Prentice-Hall , 1976, ISBN 0-13-487538-9 Kreyszig, Erwin , Advanced Engineering Mathematics 3rd, New York: Wiley , 1972, ISBN 0-471-50728-8 McGraw-Hill Encyclopedia of Science & Technology 10th. New York: McGraw-Hill . 2007. ISBN 0-07-144143-3 Moise, Edwin E., Calculus: Complete, Reading: Addison-Wesley , 1967 Protter, Murray H.; Morrey, Jr., Charles B., College Calculus with Analytic Geometry 2nd, Reading: Addison-Wesley , 1970, LCCN 76087042 Schey, H. M. Div, Grad, Curl, and All That 2nd. W. W. Norton. 1992. ISBN 0-393-96251-2OCLC 25048561 Stoker, J. J., Differential Geometry, New York: Wiley , 1969, ISBN 0-471-82825-4 Swokowski, Earl W.; Olinick, Michael; Pence, Dennis; Cole, Jeffery A., Calculus 6th, Boston: PWS Publishing Company, 1994, ISBN 0-534-93624-5 张贤达 , 《矩阵分析与应用》, 清华大学出版社, 2004, ISBN 9787302092711(中文(中国大陆))