此条目没有列出任何参考或来源。 (2018年12月18日)
维基百科所有的内容都应该可供查证。请协助补充可靠来源以改善这篇条目。无法查证的内容可能会因为异议提出而移除。 |
数学上,可导双射函数 的反函数微分可由
的反函数微分可由 的导函数
的导函数 给出。若使用拉格朗日记法,反函数
给出。若使用拉格朗日记法,反函数 [注 1]的导数公式为:
[注 1]的导数公式为:
![{\displaystyle \left[f^{-1}\right]'(a)={\frac {1}{f'\left(f^{-1}(a)\right)}},}](/media/math_img/1364/0347bdeee0d3f1ccf902a27310a5e388d8665c73.svg)
该表述等价于
![{\displaystyle {\mathcal {D}}\left[f^{-1}\right]={\frac {1}{({\mathcal {D}}f)\circ \left(f^{-1}\right)}},}](/media/math_img/1364/b71cf74aa5480ff9d43a9823ceb5580914f923a5.svg)
其中  表示一元微分算子(在函数的空间上),
表示一元微分算子(在函数的空间上), 表示二元复合算子。
表示二元复合算子。
记 ,则上式可用莱布尼兹符号写成:
,则上式可用莱布尼兹符号写成:

换言之,函数及其反函数的导数均可逆[注 2],并且乘积为1。这是链式规则的直接结果,因为

而  相对于
相对于  的导数为1。
的导数为1。
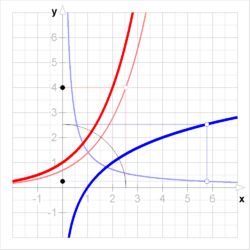
几何上,函数和反函数有关于直线 y = x.镜像的图像,这种映射将任何线的斜率变成其倒数。
假设  在
在 的邻域有一个反函数并且它在该点的导数不为零,则它的反函数保证在 x 处是可微的,并有上述公式给出的导数。
的邻域有一个反函数并且它在该点的导数不为零,则它的反函数保证在 x 处是可微的,并有上述公式给出的导数。
反函数举例
- ( 为正)具有逆 中。
-
-
但是,在 x = 0有一个问题:平方根函数图像变为垂直的,相对应平方函数的水平切线。
- ( 为实数)具有逆 ( 为正值)
-
-
其他属性
- [注 3]
可见,具有连续导数的函数(光滑函数)在其导数非零的每一点的邻域内都有反函数。如果导数不连续的,则上述积分公式不成立。
高阶导数
上面给出的链式法则是通过对等式 关于 微分得到的。对于更高阶的导数,可以继续同样的过程。对恒等式对 求导两次,得到
-
使用链式法则进一步简化为
-
用之前得到的恒等式替换一阶导数,得到
-
对三阶导数类似:
-
或者用二阶导数的公式,
-
这些公式是由Faa di Bruno公式推广。
这些公式也可以用拉格朗日表示法来表示。如果 和 是互逆的,则
-
反函数的微分举例
- 有逆运算 。使用反函数的二次导数公式,
-
于是,
- ,
与直接计算相同。
注释
参见







![{\displaystyle \left[f^{-1}\right]'(a)={\frac {1}{f'\left(f^{-1}(a)\right)}},}](/media/math_img/1364/0347bdeee0d3f1ccf902a27310a5e388d8665c73.svg)
![{\displaystyle {\mathcal {D}}\left[f^{-1}\right]={\frac {1}{({\mathcal {D}}f)\circ \left(f^{-1}\right)}},}](/media/math_img/1364/b71cf74aa5480ff9d43a9823ceb5580914f923a5.svg)





