弹性多面体

弹性多面体（或译柔性多面体[1]:27）是没有固定边界的多面体，可以不改变面的形状、不折断或弯曲任何面或边，而改变其形状。根据柯西刚性定理，在三维以及更高维度的空间中，这种多面体不能是凸的。

史特芬十四面体是目前已知结构最简单的非面自相交的弹性多面体

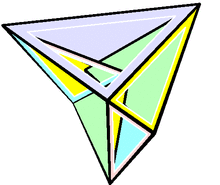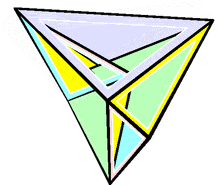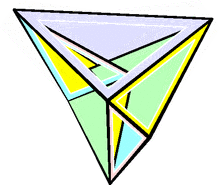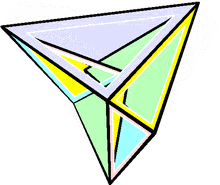
最早发现的弹性多面体为布里卡尔八面体，于1897年由拉乌尔·布里卡尔（英语：Raoul Bricard）发现[2]。其与正八面体同构，但存在自相交面，换句话说，其是一种底面为不固定形状之反平行四边形的双四角锥[3]。在空间中，不自相交的弹性多面体的例子最早由罗伯特·康奈利（英语：Robert Connelly）于1977年发现，称为康奈利形状[4]。克劳斯·史特芬（德语：Klaus Steffen）也提出了一个弹性多面体，称为史特芬十四面体，是目前已知结构最简单的非面自相交的弹性多面体[5]，并且是基于布里卡尔八面体而产生的多面体。[6]

风箱猜想

在1970年代后期罗伯特·康奈利（英语：Robert Connelly）和丹尼斯·苏利文提出了风箱猜想，认为弹性多面体在改变形状的过程体积会维持不变。后来，伊扎德·萨比托夫（俄语：Сабитов, Иджад Хакович）以消去理论（英语：Elimination theory）证明，与球同胚的多面体符合此猜想[7]。再后来，康奈利、萨比托夫和安克·沃尔兹（Anke Walz）证明了具有可定向二维表面的任何多面体都能满足此猜想。[8]该证明过程将皮耶罗·德拉·弗朗切斯卡提出的四面体体积公式[9]推广为任意多面体的体积公式。该体积公式表明，多面体的体积必为某个多项式的根，而该多项式的系数仅取决于多面体的边长。由于边长不会随着多面体的变形过程改变，因此体积必须保持在多项式的有限个根之一，而不会连续变化。[10]

切割全等

康奈利（英语：Robert Connelly）推测弹性多面体的登不变量（英语：Dehn invariant）在形变过程皆会保持不变。这被称为强风箱猜想，在2018年获证后又称为强风箱定理。[11]由于只要是同一种弹性多面体，不论其任一形变形式，体积与登不变量（英语：Dehn invariant）始终保持不变，因此不同形变形式之间必定切割全等。这意味着弹性多面体可借由分解成多个小块，重组成同一种弹性多面体的另一个形变模式。弹性多面体的平均曲率（定义为边长与外二面角的乘积之和）是登不变量（英语：Dehn invariant）的函数，且这个不变量会在弹性多面体形变时保持不变。[12]

非刚性多面体

刚性多面体是与弹性多面体多面体相对的概念，即多面体的所有面形状皆固定的情况下仅能决定唯一边界，不具备可活动性。而非刚性多面体多面体不一定是弹性多面体，部分多面体在边长不变下允许面的形状可些微改变（例如只架构多面体骨架的模型），因此其整体形状是可变的，例如耶森二十面体。这类多面体有时被称为“可活动的多面体”（shaky polyhedron）[13][14]。

参见

参考文献

  1. ^ Ian Stewart; 张云（译）. 数学万花筒2：五彩缤纷的数学问题及知识. 人民邮电出版社. ISBN 9787115264473. 
  2. ^ Bricard, R., Mémoire sur la théorie de l'octaèdre articulé, J. Math. Pures Appl., 1897, 5 (3): 113–148 [2008-07-27], （原始内容存档于2012-02-16） 
  3. ^ Gaifullin, Alexander A. Flexible polyhedra and their volumes. arXiv preprint arXiv:1605.09316. 2016. 
  4. ^ Connelly, Robert, A counterexample to the rigidity conjecture for polyhedra, Publications Mathématiques de l'IHÉS, 1977, 47 (47): 333–338 [2021-09-10], ISSN 1618-1913, MR 0488071, doi:10.1007/BF02684342, （原始内容存档于2021-01-29） 
  5. ^ Demaine, Erik D.; O'Rourke, Joseph, 23.2 Flexible polyhedra, Geometric Folding Algorithms: Linkages, origami, polyhedra, Cambridge University Press, Cambridge: 345–348, 2007, ISBN 978-0-521-85757-4, MR 2354878, doi:10.1017/CBO9780511735172 .
  6. ^ Alexandrov, Victor, The Dehn invariants of the Bricard octahedra, Journal of Geometry, 2010, 99 (1–2): 1–13, MR 2823098, arXiv:0901.2989  , doi:10.1007/s00022-011-0061-7 
  7. ^ Sabitov, I. Kh., On the problem of the invariance of the volume of a deformable polyhedron, Rossiĭskaya Akademiya Nauk. Moskovskoe Matematicheskoe Obshchestvo. Uspekhi Matematicheskikh Nauk, 1995, 50 (2): 223–224, ISSN 0042-1316, MR 1339277 
  8. ^ Connelly, Robert; Sabitov, I.; Walz, Anke, The bellows conjecture, Beiträge zur Algebra und Geometrie, 1997, 38 (1): 1–10 [2021-09-10], ISSN 0138-4821, MR 1447981, （原始内容存档于2021-07-09） 
  9. ^ Simplex Volumes and the Cayley-Menger Determinant. MathPages.com. [2021-09-10]. （原始内容存档于2013-10-06）. 
  10. ^ Demaine, Erik D.; O'Rourke, Joseph, 23.2 Flexible polyhedra, Geometric Folding Algorithms: Linkages, origami, polyhedra, Cambridge University Press, Cambridge: 345–348, 2007, ISBN 978-0-521-85757-4, MR 2354878, doi:10.1017/CBO9780511735172 
  11. ^ Gaĭfullin, A. A.; Ignashchenko, L. S., Dehn invariant and scissors congruence of flexible polyhedra, Trudy Matematicheskogo Instituta Imeni V. A. Steklova, 2018, 302 (Topologiya i Fizika): 143–160, ISBN 5-7846-0147-4, MR 3894642, doi:10.1134/S0371968518030068 
  12. ^ Alexander, Ralph, Lipschitzian mappings and total mean curvature of polyhedral surfaces. I, Transactions of the American Mathematical Society, 1985, 288 (2): 661–678, JSTOR 1999957, MR 0776397, doi:10.2307/1999957   
  13. ^ Goldberg, Michael. Unstable polyhedral structures. Mathematics Magazine. 1978, 51 (3): 165–170. JSTOR 2689996. MR 0498579. doi:10.2307/2689996. 
  14. ^ Weisstein, Eric W. (编). Shaky Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 

外部链接