双四角锥
在几何学中,双四角锥是指以四边形做为基底的双锥体,由于双锥体是由二个锥体叠起来的,因此不存在底面,因此只能讨论其基底之形状。当基底的形状为正方形时会成为双正四角锥又称为正四角双锥。若基底的形状为正方形且每个面皆为正三角形则为正八面体。所有四角柱都有8个面6个顶点和12个边。对偶多面体是四角柱。
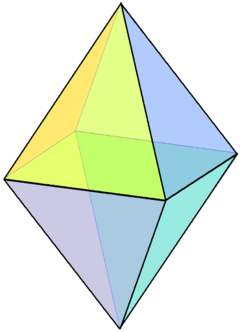 | ||
| 类别 | 双锥体 | |
|---|---|---|
| 对偶多面体 | 四角柱 | |
| 数学表示法 | ||
| 考克斯特符号 | ||
| 施莱夫利符号 | { }+{4} | |
| 康威表示法 | dP4 | |
| 性质 | ||
| 面 | 8 | |
| 边 | 12 | |
| 顶点 | 6 | |
| 欧拉特征数 | F=8, E=12, V=6 (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 8个三角形(侧面) 基底为四边形 | |
| 面的布局 | V4.4.4 | |
| 对称性 | ||
| 对称群 | D4h, [4,2], (*224), order 16 | |
| 旋转对称群 | D4, [4,2]+, (224), order 8 | |
| 特性 | ||
| 凸 | ||
| 图像 | ||
| ||
 只要基底是四边形皆称为双四角锥 |
正四角双锥
基底为正方形和且每一个面皆为正三角形的双锥体称为正四角双锥,即是正八面体,是帕雷托立体之一。
| 正四角双锥 |
长方双锥
基底为长方形的双四角锥称为长方双锥。
| 长方双锥 |
梯形双锥
基底是梯形的双四角锥称为梯形双锥
| 梯形双锥 |
凹双四角锥
凹双四角锥是指有一个角大于180度的双四角锥,通常凹双四角锥都是因为基底为凹四边形才会构成
相关多面体与镶嵌
| 对称群:[4,2], (*422) | [4,2]+, (422) | [1+,4,2], (222) | [4,2+], (2*2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| {4,2} | t{4,2} | r{4,2} | 2t{4,2}=t{2,4} | 2r{4,2}={2,4} | rr{4,2} | tr{4,2} | sr{4,2} | h{4,2} | s{2,4} |
| 半正对偶 | |||||||||
| V42 | V82 | V42 | V4.4.4 | V24 | V4.4.4 | V4.4.8 | V3.3.3.4 | V22 | V3.3.2.3 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 作为球面镶嵌 | ||||||||||||
