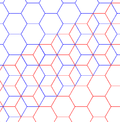
六阶六角星镶嵌

在几何学中，六阶六角星镶嵌（英语：Order-6 hexagrammic tiling）是一种正星形镶嵌，密铺于欧几里德平面，由六角星DavidStar.png以重叠密度3构成，但实际上每一个六角星内部皆无重叠，因此，六阶六角星镶嵌是一个完整的密铺，无重叠且无空隙，但其对偶二复合正六边形镶嵌有重叠，因此不能算是严格密铺，而六阶六角星镶嵌是严格密铺。

六阶六角星镶嵌
六阶六角星镶嵌
类别平面镶嵌
对偶多面体二复合正六边形镶嵌
数学表示法
考克斯特符号
（英语：Coxeter-Dynkin diagram）		node_1 6 rat 2x node 6 node 
施莱夫利符号{6/2,6}
威佐夫符号
（英语：Wythoff symbol）		6 | 6/2 2
组成与布局
顶点图(6/2)6
对称性
对称群[6,3], (*632)
图像
Compound of two hexagonal tiling.png
二复合正六边形镶嵌
（对偶多面体）

六阶六角星镶嵌在施莱夫利符号中用{6/2,6}表示，也可以计为{6|2,6}或{6/2,6}。

相关镶嵌

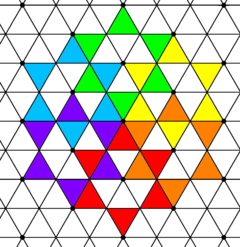
六阶六角星镶嵌和正三角形镶嵌{3,6}有相同的顶点布局

 
星形多面体和镶嵌系列：(n⁄2)n
对称群
*n32
[n,3] 		球面镶嵌 平面镶嵌 双曲镶嵌 仿紧凑 非紧凑
*532
[5,3] 		*632
[6,3] 		*732
[7,3] 		*832
[8,3] 		*932
[9,3] 		*10 32
[10,3]... 		*∞32
[∞,3] 		 
[iπ/λ,3]
考克斯特纪号                                                                
星形
顶点
布局 		 
(5⁄2)5 		 
(6⁄2)6 		 
(7⁄2)7 		 
(8⁄2)8		  
(9⁄2)9		  
(10⁄2)10		  
(∞⁄2)∞		 (∞⁄2)∞
面            
星形对偶
考克斯特纪号                                                                
星形
顶点
布局 		 
(55)∕2 		 
(66)∕2 		 
(77)∕2 		 
(88)∕2 		 
(9⁄2)9		  
(10⁄2)10		   
(偶数)(奇数)
(∞∞)∕2 		(∞∞)∕2

参见

参考文献

  • Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, Grünbaum, Branko ; and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1.  (Chapter 2.1: Regular and uniform tilings, p. 58-65)
  • Klitzing, Richard. 2D Euclidean tilings o3o6x - hexat - O3. bendwavy.org. 
  • Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979: 35. ISBN 0-486-23729-X. 
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]
  • Klitzing, Richard. 2D Euclidean tilings x3o6o - trat - O2. bendwavy.org. 
  • Tilings and Patterns, from list of 107 isohedral tilings, p.473-481