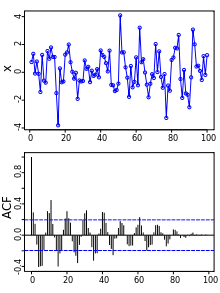
自相关函数
自相关(英语:Autocorrelation),也叫序列相关[1],是一个信号于其自身在不同时间点的互相关。非正式地来说,它就是两次观察之间的相似度对它们之间的时间差的函数。它是找出重复模式(如被噪声掩盖的周期信号),或识别隐含在信号谐波频率中消失的基频的数学工具。它常用于信号处理中,用来分析函数或一系列值,如时域信号。
定义
自相关函数在不同的领域,定义不完全等效。在某些领域,自相关函数等同于自协方差。
统计学
将一个有序的随机变量序列与其自身相比较,这就是自相关函数在统计学中的定义。每个不存在相位差的序列,都与其自身相似,即在此情况下,自相关函数值最大。如果序列中的组成部分相互之间存在相关性(不再是随机的),则由以下相关值方程所计算的值不再为零,这样的组成部分为自相关。
- ......... 期望值。
- ........ 在t(i)时的随机变量值。
- ........ 在t(i)时的预期值。
- .... 在t(i+k)时的随机变量值。
- .... 在t(i+k)时的预期值。
- ......... 为方差。
所得的自相关值R的取值范围为[-1,1],1为最大正相关值,-1则为最大负相关值,0为不相关。
信号处理
在信号处理中,上面的定义通常不进行归一化,即不减去均值并除以方差。当自相关函数由均值和方差归一化时,有时会被称作自相关系数。[2]
给定一个信号 ,连续自相关函数 通常定义为 与其自身延迟 的连续互相关。
其中 表示共轭复数, 是对函数 操作的一个函数,定义为 而 表示卷积。
对于实值函数, 。
注意积分中的参数 是一个虚变量,并且只对计算积分有用。没有具体含义。
离散信号 的延迟为 的离散自相关 是
上述定义在信号平方可积或平方可和(即有限能量)的前提下才成立。但“永远持续”的信号被处理成随机过程,就需要使用基于期望值的与之不同的定义。对于宽平稳随机过程,自相关函数定义为
对于非平稳过程,这些也会是 或者 的函数。
对于还是可遍历的过程, 期望会被换成时间平均的极限。各态历经过程的自相关函数有时定义为或等于[2]
这些定义的优点是,它们合理定义了周期函数的单变量结果,甚至当那些函数不是平稳各态历经过程时。
此外,“永远持续”的信号可以通过短时距自相关函数使用有限时间积分来处理(相关过程参见短时距傅里叶变换。)
多维自相关定义类似。例如,在三维中, 平方可和的离散信号的自相关就会是
若在求自相关函数之前从信号中减去均值,得出的函数通常称为自协方差函数。
自相关函数的性质
以下以一维自相关函数为例说明其性质,多维的情况可方便地从一维情况推广得到。
- 对称性:从定义显然可以看出R(i) = R(−i)。连续型自相关函数为偶函数
- 当f为实函数时,有:
- 当f是复函数时,该自相关函数是厄米函数,满足:
- 其中星号表示共轭。
- 周期函数的自相关函数是具有与原函数相同周期的函数。
- 两个相互无关的函数(即对于所有 τ,两函数的互相关均为0)之和的自相关函数等于各自自相关函数之和。
- 由于自相关函数是一种特殊的互相关函数,所以它具有后者的所有性质。
- 连续时间白噪声信号的自相关函数是一个δ函数,在除 τ = 0 之外的所有点均为0。
- 维纳-辛钦定理表明,自相关函数和功率谱密度函数是一对傅里叶变换对:
- 实值、对称的自相关函数具有实对称的变换函数,因此此时维纳-辛钦定理中的复指数项可以写成如下的余弦形式:
自相关函数举例
白噪声的自相关函数为δ函数:
应用
- 信号处理中,自相关可以提供关于重复事件的信息,例如音乐节拍(例如,确定节奏)或脉冲星的频率(虽然它不能告诉我们节拍的位置)。另外,它也可以用来估计乐音的音高。
参考文献
- ^ Zovko, Ilija I. Topics in Market Microstructure. Amsterdam University Press. 2008-09-01. ISBN 9789056295387 (英语).
- ^ 2.0 2.1 Dunn, Patrick F. Measurement and Data Analysis for Engineering and Science. New York: McGraw–Hill. 2005. ISBN 0-07-282538-3.