抛物柱面坐标系(英语:Parabolic cylindrical coordinates)是一种三维正交坐标系。往 z-轴方向延伸二维的抛物线坐标系 ,则可得到抛物柱面坐标系。其坐标曲面是共焦的抛物柱面。抛物柱面坐标可以应用于许多物理问题。例如,物体边缘的位势论。

抛物柱面坐标系的几个坐标曲面。红色抛物柱面的

。黄色抛物柱面的

。蓝色薄面的

。z-轴是垂直的,以白色表示。 x-轴以绿色表示。三个曲面相交于点 P (显示为黑色的圆球),
直角坐标大约为

。
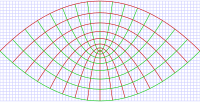
抛物线坐标系的

和

的等值曲线。横轴与纵轴分别为 x-轴与 y-轴。抛物线坐标系可以往 z-轴延伸。对于任意 z-坐标,这曲线图都正确无误。
基本定义
直角坐标 可以用抛物柱面坐标 表示为
- 、
- 、
- ;
其中, , 。
坐标 为常数的曲线形成共焦的,凹性往 +y-轴的抛物柱面:
- ,
而坐标 为常数的曲线形成共焦的,凹性往 -y-轴的抛物柱面:
- 。
这些抛物柱面的焦线的位置都在 z-轴。
径向距 的公式为
- 。
当解析经典力学的反平方连心力问题时,假若采用抛物柱面坐标的哈密顿-亚可比方程式,则会用到这很有用的公式。参阅
拉普拉斯-龙格-冷次向量。
标度因子
抛物柱面坐标 与 的标度因子相等;而 的标度因子是 1 :
- 、
- 。
无穷小体积元素是
- 。
拉普拉斯算子是
- 。
其它微分算子,像 、 ,都可以用 坐标表示,只要将标度因子代入在正交坐标系条目内对应的一般公式。
应用
抛物柱面坐标有一个经典的应用,这是在解析像拉普拉斯方程或亥姆霍兹方程这类的偏微分方程式。在这些方程式里,抛物柱面坐标允许分离变数法的使用。个典型的例题是,有一块半无限的平板导体,请问其周围的电场为什么?应用抛物柱面坐标,我们可以精致地分析这例题。
参阅
参考文献
- Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 181. ASIN B0000CKZX7.
- Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 96.
- Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9. Same as Morse & Feshbach (1953), substituting uk for ξk。
- Moon P, Spencer DE. Parabolic-Cylinder Coordinates (μ, ν, z). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 21–24 (Table 1.04). ISBN 978-0387184302.
外部链接







