扁球面坐标系(英语:Oblate spheroidal coordinates)是一种三维正交坐标系。设定二维椭圆坐标系包含于xz-平面;两个焦点 与
与 的直角坐标分别为
的直角坐标分别为 与
与 。将椭圆坐标系绕着z-轴旋转,则可以得到扁球面坐标系。(假若,绕着y-轴旋转,则可以得到长球面坐标系。)椭圆坐标系的两个焦点,变为一个半径为
。将椭圆坐标系绕着z-轴旋转,则可以得到扁球面坐标系。(假若,绕着y-轴旋转,则可以得到长球面坐标系。)椭圆坐标系的两个焦点,变为一个半径为 的圆圈,包含于三维空间的xy-平面。称这圆圈为焦圆,又称为参考圆。扁球面坐标系可以被视为椭球坐标系的极限案例,其两个最大的半轴的长度相同。
的圆圈,包含于三维空间的xy-平面。称这圆圈为焦圆,又称为参考圆。扁球面坐标系可以被视为椭球坐标系的极限案例,其两个最大的半轴的长度相同。
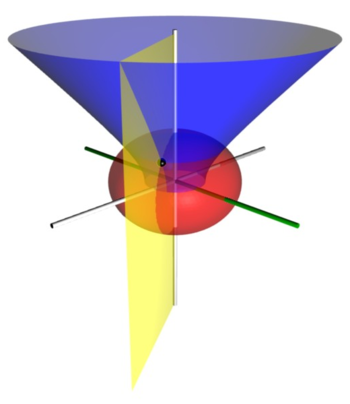
图1)扁球面坐标系的几个
坐标曲面。红色扁球面的

。蓝色半双曲面的

。黄色半平面的

(黄色半平面与xz-半平面之间的
二面角角度是

)。z-轴是垂直的,以白色表示。x-轴以绿色表示。三个坐标曲面相交于点P(以黑色的圆球表示),
直角坐标大约为

。
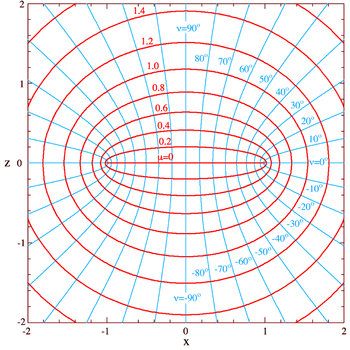
图2)椭圆坐标系绘图。横轴是x-轴,竖轴是z-轴。红色椭圆(

-等值线)变成上图的红色扁球面(

坐标曲面),而

青蓝色双曲线(

-等值线)则变成蓝色半双曲面(

坐标曲面)。
当边界条件涉及扁球面或旋转双曲面时,扁球面坐标时常可以用来解析偏微分方程式。例如,关于佩兰摩擦因子(Perrin friction factors)的计算,扁球面坐标扮演了极重要的角色。让·佩兰因此而荣获1926年诺贝尔物理奖。佩兰摩擦因子决定了分子的旋转扩散(rotational diffusion)。这程序又影响了许多科技,像蛋白质核磁共振光谱学(protein NMR),的可行性。应用这程序,我们可以推论分子的流体动力体积与形状。扁球面坐标也时常用来解析电磁学(例如,扁球形带电的分子的电容率),声学(例如,声音通过圆孔时产生的散射),流体动力学(水通过消防水带的喷口),扩散理论(红热的钱币在水里的冷却),等等方面的问题。
第一种表述
在三维空间里,一个点P的扁球面坐标 常见的定义是
- 、
- 、
- 。
其中, 是个实数,角度 ,角度 。
学术界比较中意这一种扁球面坐标,因为没有简并;三维空间内每一点都拥有自己独特的扁球面坐标。
坐标曲面
坐标曲面是扁球面 :
- 。
它们是由椭圆绕着z-轴旋转形成的。椭球面与xz-平面的相交,是一个的椭圆。沿着x-轴,长半轴长度为 ,沿着z-轴,短半轴长度为 。椭圆的焦点都包含于x-轴,x-坐标分别为 。
坐标曲面是半个单叶旋转双曲面 :
- 。
假若 是正值, 也是正值,这半个单叶旋转双曲面在xy-平面以上;假若是负值,则在xy-平面以下。 是双曲线的渐近线的角度。所有双曲线的焦点都在x-轴,x-坐标分别为 。
坐标曲面是个半平面 :
- 。
逆变换
用直角坐标 来计算扁球面坐标 ,方位角 的公式为
- 。
设定 与 分别为点P与焦圆的最远距离与最近距离,以方程式表示为
- 、
- 。
坐标 和 的方程式分别为
- 、
- 。
标度因子
扁球面坐标 与 的标度因子相等:
- 。
方位角 的标度因子为
- 。
无穷小体积元素是
- 。
拉普拉斯算子是
- 。
其它微分算子,像 、 ,都可以用 坐标表示,只要将标度因子代入在正交坐标系条目内对应的一般公式。
第二种表述
另外有一组有时会用到的扁球面坐标 ;其中, , [1]。 坐标曲面是个扁球面, 坐标曲面是个旋转双曲面。从直角坐标变换至扁球面坐标:
- 、
- 、
- 。
其中,实数 ,实数 ,角度 。
标度因子
扁球面坐标 的标度因子分别为:
- 、
- 、
- 。
无穷小体积元素是
- 。
拉普拉斯算子是
- 。
第三种表述
图3)第三种扁球面坐标系
的三个
坐标曲面。红色扁球面是
坐标曲面。蓝色单叶双曲面是
坐标曲面。黄色半平面是
坐标曲面 (黄色半平面与xz-半平面之间的
二面角角度是
)。z-轴是垂直的,以白色表示。x-轴以绿色表示。第三种扁球面坐标系有双重简并。这可以从三个坐标曲面的两个相交点P
1,P
2 (以黑色的圆球表示)观察到。
另外,还有一种比较有几何直觉性的扁球面坐标系 [2]:
- 、
- 、
- 。
坐标 必须大于或等于1。坐标 必须在正负1之间。 坐标曲面是扁球面。 坐标曲面是单叶双曲面,包含了对应于正负 的半双曲面。第三种坐标有双重简并:三维空间的两点(直角坐标 映射至一组扁球面坐标系 )。这双重简并可以从直角坐标变换至扁球面坐标的公式观察到:
- 、
- 、
- 。
坐标 与 有一个简单的公式来表达任何一点P与焦圆的最远距离 ,最近距离 :
- 、
- 。
所以,点P与焦圆的最远距离是 ,点P与焦圆的最近距离是 。
坐标曲面
坐标曲面是扁球面 :
- 。
坐标曲面是单叶旋转双曲面 :
- 。
坐标曲面是半个平面 :
- 。
标度因子
扁球面坐标 的标度因子分别为:
- 、
- 、
- 。
无穷小体积元素是
- 。
拉普拉斯算子是
- 。
其它微分算子,像 、 ,都可以用 坐标表示,只要将标度因子代入在正交坐标系条目内对应的一般公式。
如同球坐标解答的形式为球谐函数,拉普拉斯方程可以用分离变数法来求解,得到形式为扁球谐函数的答案。假若,边界条件涉及扁球面,我们可以优先选择这方法来解析。
参阅
参考文献
- ^ Smythe, 1968。
- ^ Abramowitz and Stegun, p. 752。
参考目录
不按照命名常规
- Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 662. 采用 、 、 。
- Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 115. ISBN 0-86720-293-9. 如同Morse & Feshbach (1953),采用 来替代 。
- Smythe, WR. Static and Dynamic Electricity 3rd ed. New York: McGraw-Hill. 1968.
- Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 98. 采用混合坐标 、 、 。
按照命名常规
- Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 177. 采用第一种表述 ,又加介绍了简并的第三种表述 。
- Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: p. 182. 如同Korn and Korn (1961),但采用余纬度 来替代纬度 。
- Moon PH, Spencer DE. Oblate spheroidal coordinates (η, θ, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer Verlag. 1988: pp. 31–34 (Table 1.07). ISBN 0-387-02732-7. Moon and Spencer采用余纬度常规 ,又改名 为 。
特异命名常规
- Landau LD, Lifshitz EM, Pitaevskii LP. Electrodynamics of Continuous Media (Volume 8 of the Course of Theoretical Physics) 2nd edition. New York: Pergamon Press. 1984: pp. 19–29. ISBN 978-0750626347. 视扁球面坐标系为椭球坐标系的极限。采用第二种表述。














