此条目需要精通或熟悉相关主题的编者参与及协助编辑。 (2014年4月8日)
请邀请适合的人士改善本条目。更多的细节与详情请参见讨论页。 |
设A为一个有n个数字的有序集(n>1),其中所有数字各不相同。
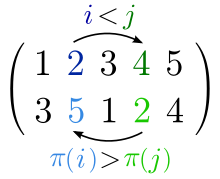
一个排列逆序对的突显,它可以由序位(2,4)或对位元素(5,2)表示。
如果存在正整数i, j使得1 ≤ i < j ≤ n而且A[i] > A[j],则<A[i], A[j]>这一个有序对称为A的一个逆序对,也称作逆序。逆序对的数量称作“逆序数”[1]或“反序数”[2]。
例如:数组<2,3,8,6,1>的逆序对为:<2,1> <3,1> <8,1> <8,6> <6,1>共5个逆序对。
对于<2,1>:1 ≤ 1 < 5 ≤ 5 ,A[1] >A[5],所以<A[1],A[5]>为一个合法的逆序对。
目前求逆序对数目比较普遍的方法是利用归并排序做到 的时间复杂度。
的时间复杂度。
当然,也可以利用树状数组、线段树来实现这种基础功能。复杂度均为 。
。
定义
逆序
设 为一个排列,如果 而且 ,
这个序位 或这一对元素 被称为是 的一个逆序。通常逆序是对于排列的定义,但也可以用于序列:
设 是一个序列(或多重排列)。如果 而且 ,
这个序位 或这对元素 被称为是 的一个逆序。
对于根据元素组成的序列,逆序的定义不是唯一的,因为不同的序位上可能有相同的值对。逆序集是所有逆序的集合。一个排列依其序位而定义的逆序集是,它的反向排列依其序位而定义的逆序集,反之亦然,只是交换了配对的元素。
逆序数
逆序数是逆序集的基数,它常用于量度排列或序列的已排序程度。
在一个排列的箭头指向图中,它是箭头指向相交叉的数,也是从自指(identity)排列而得到的Kendall tau距离,以及每个反向相关向量的和,如下列定义。
对于逆序数,依序位或依元素而定义的分别并不重要,因为排列及其反向排列都具有相同的逆序数。
其它测量(预先)排序程度的方式,包括了为排好序列而从序列中可以删除元素的最小数量,对序列所“进行”排序的次数和长度,每个元素在已排序位置之上的距离总和(Spearman footrule),以及排序过程中必需的最少交换次数。比较排序算法计算逆序数的时间为O(n log n)。
相关联的逆序向量
有三个类似的向量用于将排列的逆序,压缩到确定唯一的向量中。它们通常被称为逆序向量或Lehmer码。本文将逆序向量记为( ),其它的两个向量有时分别称为左和右逆序向量;为了避免与前面的逆序向量混淆,本文将另两个分别称为左逆序计数 和右逆序计数 。左逆序计数是以反向colexicographic次序的排列,右逆序计数则是以字典次序的排列。
- 逆序向量 :依据元素的定义, 是较小(右)分量为 的逆序数。 是在 之中的 之前,元素较 大的数量。
-
- 左逆序计数 :依据位置的定义, 是较大(右)分量为 的逆序数。 是在 之中的 之前,元素较 大的数量。
-
- 右逆序计数 ,通常称为Lehmer码:依据位置的定义, 是较小(左)分量为i的逆序数。 是 之中的 之后,元素较 小的数量。
-
Rothe图可以协助找出 和 。Rothe图是以黑点来表示1的排列矩阵,每一个位置上若为逆序(通常以叉号表示)则在其右侧与下方即有一点。 是图中第 列排列逆序的加总,而 是 栏中排列逆序的加总。排列矩阵的倒反即是此矩阵的转置,因此某一排列的 即是它转置的 ,反之亦然。
范例:四个元素的全部排列
下面可排序表显示了四个元素的集合,它的逆序集会有不同位置的24种排列、逆序相关向量和逆序数(右栏是它的反向排列,用于以colex排序)。可以看出 和 的位数总是相同,而 和 与位逆序集有关。
最右侧栏是排列左上右下对角线的总和,如三角形图示,以及r是左下右上对角线的总和(配对在下降对角线中其右侧都是2,3,4组成,而在上升对角线中的左侧都是1,2,3组成)。
此表中 的预设排序是反向colex次序,这与 的colex次序相同。 的字典序与 的字典序相同。
| 三个元素的全部排列表
|
|---|
|
|
|
|
|
|
|
|
|
|
p-b
|
|
|
#
|
|---|
| 0 |
|
123 |
321 |
000 |
000 |
000 |
000 |
|
000 |
000 |
0
| | 1 |
|
213 |
312 |
100 |
001 |
010 |
010 |
|
100 |
001 |
1
| | 2 |
|
132 |
231 |
010 |
010 |
100 |
001 |
|
010 |
010 |
1
| | 3 |
|
312 |
213 |
110 |
011 |
110 |
011 |
|
200 |
002 |
2
| | 4 |
|
231 |
132 |
200 |
002 |
200 |
002 |
|
110 |
011 |
2
| | 5 |
|
321 |
123 |
210 |
012 |
210 |
012 |
|
210 |
012 |
3
|
|
|
| 四个元素的全部排列表
|
|---|
|
|
|---|
| 0
| | 1
| | 2
| | 3
| | 4
| | 5
| | 6
| | 7
| | 8
| | 9
| | 10
| | 11
| | 12
| | 13
| | 14
| | 15
| | 16
| | 17
| | 18
| | 19
| | 20
| | 21
| | 22
| | 23
|
|
|
|
|
|
|
|
|
|
p-b
|
|
|
#
|
|---|
| 0 |
|
1234 |
4321 |
0000 |
0000 |
0000 |
0000 |
|
0000 |
0000 |
0
| | 1 |
|
2134 |
4312 |
1000 |
0001 |
0010 |
0100 |
|
1000 |
0001 |
1
| | 2 |
|
1324 |
4231 |
0100 |
0010 |
0100 |
0010 |
|
0100 |
0010 |
1
| | 3 |
|
3124 |
4213 |
1100 |
0011 |
0110 |
0110 |
|
2000 |
0002 |
2
| | 4 |
|
2314 |
4132 |
2000 |
0002 |
0200 |
0020 |
|
1100 |
0011 |
2
| | 5 |
|
3214 |
4123 |
2100 |
0012 |
0210 |
0120 |
|
2100 |
0012 |
3
| | 6 |
|
1243 |
3421 |
0010 |
0100 |
1000 |
0001 |
|
0010 |
0100 |
1
| | 7 |
|
2143 |
3412 |
1010 |
0101 |
1010 |
0101 |
|
1010 |
0101 |
2
| | 8 |
|
1423 |
3241 |
0110 |
0110 |
1100 |
0011 |
|
0200 |
0020 |
2
| | 9 |
|
4123 |
3214 |
1110 |
0111 |
1110 |
0111 |
|
3000 |
0003 |
3
| | 10 |
|
2413 |
3142 |
2010 |
0102 |
1200 |
0021 |
|
1200 |
0021 |
3
| | 11 |
|
4213 |
3124 |
2110 |
0112 |
1210 |
0121 |
|
3100 |
0013 |
4
| | 12 |
|
1342 |
2431 |
0200 |
0020 |
2000 |
0002 |
|
0110 |
0110 |
2
| | 13 |
|
3142 |
2413 |
1200 |
0021 |
2010 |
0102 |
|
2010 |
0102 |
3
| | 14 |
|
1432 |
2341 |
0210 |
0120 |
2100 |
0012 |
|
0210 |
0120 |
3
| | 15 |
|
4132 |
2314 |
1210 |
0121 |
2110 |
0112 |
|
3010 |
0103 |
4
| | 16 |
|
3412 |
2143 |
2200 |
0022 |
2200 |
0022 |
|
2200 |
0022 |
4
| | 17 |
|
4312 |
2134 |
2210 |
0122 |
2210 |
0122 |
|
3200 |
0023 |
5
| | 18 |
|
2341 |
1432 |
3000 |
0003 |
3000 |
0003 |
|
1110 |
0111 |
3
| | 19 |
|
3241 |
1423 |
3100 |
0013 |
3010 |
0103 |
|
2110 |
0112 |
4
| | 20 |
|
2431 |
1342 |
3010 |
0103 |
3100 |
0013 |
|
1210 |
0121 |
4
| | 21 |
|
4231 |
1324 |
3110 |
0113 |
3110 |
0113 |
|
3110 |
0113 |
5
| | 22 |
|
3421 |
1243 |
3200 |
0023 |
3200 |
0023 |
|
2210 |
0122 |
5
| | 23 |
|
4321 |
1234 |
3210 |
0123 |
3210 |
0123 |
|
3210 |
0123 |
6
|
|
|
排列的弱次序
n物品排列的集合其部分次序的结构,称为排列的弱次序,而构成格。
以逆序集的子集关系绘出的哈斯图,则构成了称为permutohedron的骨架。
如果依位置将某一排列分配给每个逆序集,所得到的排序是permutohedron的次序,其中的边对应于连续两元素的交换。这是排列的弱排序。The identity is its minimum, and the permutation formed by reversing the identity is its maximum.
如果依元素将某一排列分配给每个逆序集,所得到的排序将是凯莱图的次序,其中的边对应于连续两元素的交换。对称组的凯莱图与其permutohedron相似,但是每个排列由其反向替换。
另见
参考
- ^ 王慧; 于海波. 线性代数. 上海: 上海交通大学出版社. 2018: 4.
- ^ 高金泰. 高等代数考研600题精解. 成都: 西南交通大学出版社. 2017: 31.