凯莱图

假设${\displaystyle G}$ 是群，而${\displaystyle S}$ 是G的生成集。凯莱图${\displaystyle \Gamma =\Gamma (G,S)}$ ，是如下构造的着色的有向图：

• ${\displaystyle G}$ 的每个元素${\displaystyle g}$ 对应一个顶点。换言之，图${\displaystyle \Gamma }$ 的顶点集合${\displaystyle V(\Gamma )}$ 视为与${\displaystyle G}$ 等同；
• ${\displaystyle S}$ 中每个生成元${\displaystyle s}$ ，对应一种颜色${\displaystyle c_{s}}$ ；
• 对于任何${\displaystyle g\in G,s\in S}$ ，画一条由元素${\displaystyle g}$ 至${\displaystyle gs}$ 的有向边，染成${\displaystyle c_{s}}$ 色。换言之，边集合${\displaystyle E(\Gamma )}$ 由形如${\displaystyle (g,gs)}$ 的有序对构成，边的颜色由${\displaystyle s\in S}$ 确定。

在几何群论中，集合${\displaystyle S}$ 通常取为有限、对称（即满足${\displaystyle S=S^{-1}}$ ），并且不包含这个群的单位元${\displaystyle e}$ 。在这种情况下，凯莱图是简单无向图：它的边没有方向（由对称性），并且不包含自环（因为${\displaystyle e\notin S}$ ）。

• 假设${\displaystyle G=\mathbb {Z} }$ 是无限循环群（即整数的加法群），而集合${\displaystyle S}$ 由标准生成元${\displaystyle 1}$ 和它的逆元（用加法符号为${\displaystyle -1}$ ）构成，则它的凯莱图是无穷链（英语：Path graph）。
• 类似地，如果${\displaystyle G=\mathbb {Z} _{n}}$ 是${\displaystyle n}$ 阶循环群（模${\displaystyle n}$ 的加法群），而${\displaystyle S}$ 仍由${\displaystyle G}$ 的标准生成元${\displaystyle 1}$ 与逆元${\displaystyle -1}$ 构成，则凯莱图是环图${\displaystyle C_{n}}$ 。
• 群的直积的凯莱图（新生成集取为原生成集之笛卡尔积），是对应的凯莱图的笛卡尔积（英语：Cartesian product of graphs）。因此阿贝尔群${\displaystyle \mathbb {Z} ^{2}}$ ，关于四个元素${\displaystyle (\pm 1,\pm 1)}$ 组成的生成集的凯莱图，是平面${\displaystyle \mathbb {R} ^{2}}$ 上的无穷网格，而带有类似的生成集的直积${\displaystyle \mathbb {Z} _{n}\times \mathbb {Z} _{m}}$ 的凯莱图，是环面上的${\displaystyle n}$ 乘${\displaystyle m}$ 有限网格。
• 二面体群${\displaystyle D_{4}}$ 有群展示：
  $${\displaystyle \langle a,b|a^{4}=b^{2}=e,ab=ba^{3}\rangle .}$$

   
  左图是关于两个生成元${\displaystyle a}$ 和${\displaystyle b}$ 的凯莱图，其中红色箭头表示左乘元素${\displaystyle a}$ （顺时针旋转${\displaystyle 90^{\circ }}$ ）。而因为元素${\displaystyle b}$ （左右反射）自反，所以表示左乘元素${\displaystyle b}${\displaystyle b}  的蓝色线是无方向的，故左图混合了有向边与无向边：它有${\displaystyle 8}$ 个顶点、${\displaystyle 8}$ 条有向边、${\displaystyle 4}$ 条无向边。
   

  二面体群${\displaystyle D_4}${\displaystyle D_{4}}  关于两个生成元${\displaystyle a}$ 和${\displaystyle b}$ 的凯莱图。
   

  ${\displaystyle D_{4}}$ 关于两个自反生成元的凯莱图
  同一个群${\displaystyle D_{4}}$ ，亦可画出不同的凯莱图，如右图。${\displaystyle b}$ 仍表示左右反射，而${\displaystyle c}$ 则是关于主对角线的反射，以粉红色线表示。由于两个反射皆自反，右边的凯莱图完全无向。对应的群展示是
  $${\displaystyle \langle b,c\mid b^{2}=c^{2}=e,bcbc=cbcb\rangle .}$$

   
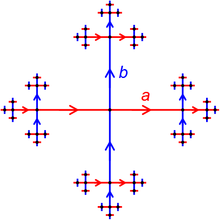
• 条目开头的图，是两个生成元${\displaystyle a,b}$ 上的自由群，关于生成集合${\displaystyle S=\{a,b,a^{-1},b^{-1}\}}$ 的凯莱图，而正中央的黑点，是单位元${\displaystyle e}$ 。沿着边向右走表示右乘${\displaystyle a}$ ，而沿着边向上走表示乘以${\displaystyle b}$ 。因为自由群没有关系，它的凯莱图中没有环。这个凯莱图是证明巴拿赫-塔斯基悖论的关键。
• 右边有离散海森堡群
   

  海森堡群的一部分（颜色仅为方便看清分层）

群${\displaystyle G}$ 通过左乘作用在自身上（参见凯莱定理）。这个作用可以看作${\displaystyle G}$ 作用在它的凯莱图上。明确而言，一个元素${\displaystyle h\in G}$ 映射一个顶点${\displaystyle g\in V(\Gamma )}$ 到另一个顶点${\displaystyle hg\in V(\Gamma )}$ 。凯莱图的边集合被这个作用所保存：边${\displaystyle (g,gs)}$ 变换成边${\displaystyle (hg,hgs)}$ 。任何群在自身上的左乘作用是简单传递的，特别是凯莱图是顶点传递（英语：Vertex-transitive graph）的。事实上，反向的结论也成立，即有下列等价刻划，称为扎比杜西定理（英语：Sabidussi's Theorem）：

（无标记又无着色）有向图${\displaystyle \Gamma }$ 是群${\displaystyle G}$ 的某个凯莱图，当且仅当${\displaystyle G}$ 可作为图自同构（就是要保存边的集合）作用在${\displaystyle \Gamma }$ 上，且该作用简单传递。^[1]

要从一个凯莱图${\displaystyle \Gamma =\Gamma (G,S)}$ 找回群${\displaystyle G}$ 和生成集${\displaystyle S}$ ，先选择一个顶点${\displaystyle v_{1}\in V(\Gamma )}$ ，标上群的单位元${\displaystyle e}$ 。接着，对${\displaystyle \Gamma }$ 的每个顶点${\displaystyle v}$ ，${\displaystyle G}$ 中有唯一元素将${\displaystyle v_{1}}$ 变换到${\displaystyle v}$ ，于是可以在${\displaystyle v}$ 处标记该唯一元素。最后要确定${\displaystyle G}$ 的哪个生成集${\displaystyle S}$ ，产生凯莱图${\displaystyle \Gamma }$ ，而所求的${\displaystyle S}$ 就是毗连${\displaystyle v_{1}}$ 的顶点标记的集合。生成集合是有限（这是凯莱图的共同假定）当且仅当这个图是局部有限的（就是说每个顶点仅毗连于有限多条边）。

• 如果生成集合的成员${\displaystyle s}$ 是自身的逆元，即${\displaystyle s=s^{-1}}$ ，则它一般被表示为无向边。
• 凯莱图${\displaystyle \Gamma (G,S)}$ 本质上依赖于如何选择生成集${\displaystyle S}$ 。例如，如果生成集合${\displaystyle S}$ 有${\displaystyle k}$ 个元素，则凯莱图的每个顶点都有${\displaystyle k}$ 条有向边进入，${\displaystyle k}$ 条有向边外出。当生成集合${\displaystyle S}$ 为对称集，且有${\displaystyle r}$ 个元素时，凯莱图是${\displaystyle r}$ 度的正则图。
• 在凯莱图中的环（“闭合路径”）指示${\displaystyle S}$ 的元素之间的关系。在群的凯莱复形此一更复杂的构造中，对应于关系的闭合路径被用多边形“填充”。
• 如果${\displaystyle f:G'\to G}$ 是满射群同态并且${\displaystyle G'}$ 的生成集合${\displaystyle S'}$ 的元素的像是不同的，则导出图覆叠（英语：Covering graph）映射
  $${\displaystyle {\bar {f}}:\Gamma (G',S')\to \Gamma (G,S),\quad }$$

   
  这里的${\displaystyle S=f(S')}$ ，特别是，如果群${\displaystyle G}$ 有${\displaystyle k}$ 个生成元，阶均不为${\displaystyle 2}$ ，并且这些生成元和它们的逆元构成集合${\displaystyle S}$ ，则该集合生成的自由群${\displaystyle F(S)}$ 有到${\displaystyle G}$ 的满同态（商映射），故${\displaystyle \Gamma (G,S)}$ 被自由群的凯莱图覆盖，即${\displaystyle 2k}$ 度的无限正则树。
• 即使集合${\displaystyle S}$ 不生成群${\displaystyle G}$ ，仍可以构造图${\displaystyle \Gamma (G,S)}$ 。但是，此情况下，所得的图并不连通。在这种情况下，这个图的每个连通分支对应${\displaystyle S}$ 所生成子群的一个陪集。
• 对于有限凯莱图（视为无向），其顶点连通性等于这个图的度的${\displaystyle 2/3}$ 。若生成集极小（即移除任一元素及其逆元，就不再生成整个群），则其顶点连通性等于度数。^[2]至于边连通性，则在任何情况下皆等于度数。^[3]
• 群${\displaystyle G}$ 的每个乘性特征标（英语：Multiplicative character）${\displaystyle \chi }$ 都给出${\displaystyle \Gamma (G,S)}$ 邻接矩阵的特征向量。若${\displaystyle G}$ 为交换群，则对应的特征值为${\displaystyle \lambda _{\chi }=\sum _{s\in S}\chi (s).}$ 特别地，平凡特征标（将所有元素映至常数${\displaystyle 1}$ ）对应的特征值，等于${\displaystyle \Gamma (G,S)}$ 的度数，即${\displaystyle S}$ 的元素个数。若${\displaystyle G}$ 为交换群，则恰有${\displaystyle |G|}$ 个特征标，故已足以确定全部特征值。

如果转而把顶点作为固定子群${\displaystyle H}$ 的右陪集，就得到了一个有关的构造Schreier陪集图，它是陪集枚举或Todd-Coxeter算法的基础。

研究图的邻接矩阵特别是应用谱图理论的定理能洞察群的结构。

• 群的生成集合
• 群的展示