肾形线

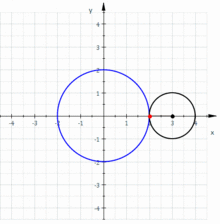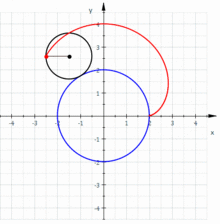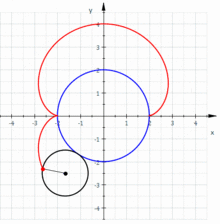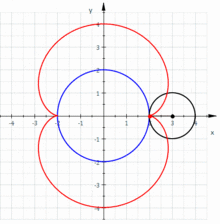
考虑一小圆在一固定圆的外面滚动，若小圆的半径为${\displaystyle a}$ ，固定圆的圆心在${\displaystyle (0,0)}$ ，半径为${\displaystyle 2a}$ ，小圆的滚动角为${\displaystyle 2\varphi }$ ，启始点为${\displaystyle (2a,0)}$ （如图所示），则可以得到肾形线的

• 参数式

${\displaystyle x(\varphi )=3a\cos \varphi -a\cos 3\varphi =6a\cos \varphi -4a\cos ^{3}\varphi \ ,}$ 

${\displaystyle y(\varphi )=3a\sin \varphi -a\sin 3\varphi =4a\sin ^{3}\varphi \ ,\qquad 0\leq \varphi <2\pi }$ 

将 ${\displaystyle x(\varphi )}$  和 ${\displaystyle y(\varphi )}$  代入以下方程

• ${\displaystyle (x^{2}+y^{2}-4a^{2})^{3}=108a^{4}y^{2}}$ 

可知上述方程即为肾形线的隐函数表示式（英语：Implicit curve）。

若尖点是在Y轴上，则参数式为

${\displaystyle x=3a\cos \varphi +a\cos 3\varphi ,\quad y=3a\sin \varphi +a\sin 3\varphi ).}$ 

隐函数表示式为

${\displaystyle (x^{2}+y^{2}-4a^{2})^{3}=108a^{4}x^{2}.}$ 

上述的肾形线，有以下的性质

• 弧长为${\displaystyle L=24a,}$ 
• 面积为${\displaystyle A=12\pi a^{2}\ }$ 
• 曲率半径为 ${\displaystyle \rho =|3a\sin \varphi |.}$ 

• Arganbright, D., Practical Handbook of Spreadsheet Curves and Geometric Constructions, CRC Press, 1939, ISBN 0-8493-8938-0, p. 54.
• Borceux, F., A Differential Approach to Geometry: Geometric Trilogy III, Springer, 2014, ISBN 978-3-319-01735-8, p. 148.
• Lockwood, E. H., A Book of Curves, Cambridge University Press, 1961, ISBN 978-0-521-0-5585-7, p. 7.

• Mathworld: nephroid （页面存档备份，存于互联网档案馆）
• Xahlee: nephroid （页面存档备份，存于互联网档案馆）