代数图论

使用线性代数

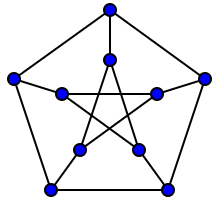
代数图论的第一个分支用线性代数来研究图，特别是研究图的邻接矩阵或拉普拉斯矩阵的谱（这部分代数图论也被称为谱图理论）。以佩特森图为例，邻接矩阵的谱为(-2, -2, -2, -2, 1, 1, 1, 1, 1, 3)。通过一些定理把谱的性质与图的其他性质联系起来。举一个简单的例子，对于直径为D的连通图，它的谱至少有D+1个不同的值^[1]。图的谱可用于分析网络的同步。

使用群论

代数图论的第二个分支用群论来研究图，尤其是自同构群以及几何群论。重点是根据对称性对图进行分类，以及不同类别之间的包含关系。某些特殊类别的图足够少，可以把它们列举出来。根据Frucht定理，所以的群都可以表示成连通图的自同构群^[2]。另外，给定一个群，可以作出相应的凯莱图，凯莱图有一些性质与群的结构相关^[1]。

代数图论的第二个分支与第一个分支有联系，因为图的对称性在图的谱中也有反映。尤其是，对于高度对称的图，例如佩特森图，不同的特征值的数目很少^[1]（佩特森图有3个不同的特征值，在直径相等的图中是最少的）。凯莱图的谱与群的结构直接相关，尤其是与不可约特征标相关^[1][3]。

研究图不变量

最后，代数图论的第三个分支研究图不变量的代数性质，尤其是色多项式、Tutte多项式与扭结不变量。例如，图的色多项式计算了顶点着色的个数。佩特森图的色多项式为${\displaystyle t(t-1)(t-2)(t^{7}-12t^{6}+67t^{5}-230t^{4}+529t^{3}-814t^{2}+775t-352)}$ ^[1]。这意味着佩特森图不能用1种或2种颜色着色，但可以用3种颜色着色，且着色方式有120种。代数图论的这一领域的许多工作都是为了证明四色定理而启发。可是仍然有许多未解决的问题，例如如何判定两个图的色多项式相同，以及如何判定一个多项式是不是某个图的色多项式。

• 谱图理论
• 代数组合学
• 代数连通度
• 邻接矩阵

1. ^ ^{1.0 1.1 1.2 1.3 1.4} Biggs, Norman (1993), Algebraic Graph Theory (2nd ed.), Cambridge: Cambridge University Press, ISBN 0-521-45897-8
2. ^ R. Frucht. Graphs of Degree 3 with given abstract group, Can. J. Math. 3 1949.
3. ^ Babai, L (1996), "Automorphism groups, isomorphism, reconstruction", in Graham, R; Grötschel, M; Lovász, L, Handbook of Combinatorics, Elsevier

• Godsil, Chris; Royle, Gordon (2001), Algebraic Graph Theory, Graduate Texts in Mathematics, 207, New York: Springer-Verlag.