圆环坐标系(英语:Toroidal coordinates)是一种三维正交坐标系。设定二维椭圆坐标系包含于 xz-平面;两个焦点  与
与  的直角坐标分别为
的直角坐标分别为  与
与  。将双极坐标系绕着 z-轴旋转,则可以得到圆环坐标系。双极坐标系的两个焦点,变为一个半径为
。将双极坐标系绕着 z-轴旋转,则可以得到圆环坐标系。双极坐标系的两个焦点,变为一个半径为  的圆圈,包含于圆环坐标系的 xy-平面。称这圆圈为焦圆,又称为参考圆。
的圆圈,包含于圆环坐标系的 xy-平面。称这圆圈为焦圆,又称为参考圆。
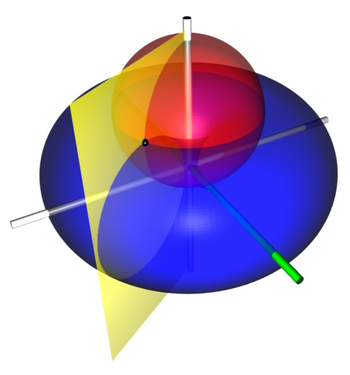
图 1 )圆环坐标系的几个
坐标曲面。红色圆球面的

。蓝色环面的

。黄色半平面的

。z-轴是垂直的,以白色表示。 x-轴以绿色表示。三个坐标曲面相交于点 P (以黑色的圆球表示),
直角坐标大约为

。
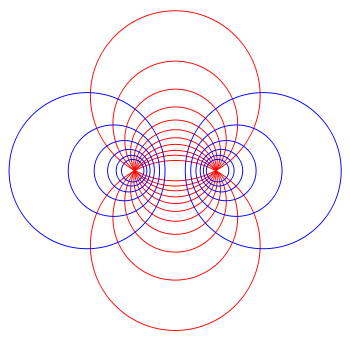
图 2 )双极坐标系绘图。红色圆圈变成上图的红色圆球面(

-坐标曲面),而蓝色圆圈则变成蓝色环面(

-坐标曲面)。
在三维空间里,一个点 P 的圆环坐标 最常见的定义是
- 、
- 、
- ;
其中, 是直角坐标, 坐标是 的弧度, 坐标是点 P 离两个焦点的距离 与 的比例的自然对数:
- 。
圆环坐标的值域为 , , 。
坐标曲面
每一个 -坐标曲面都是包含了焦圆,而不同心的圆球面。圆球半径为
- 。
正值 的圆球面的圆心都在正 z-轴;而负值 的圆球面的圆心则在负 z-轴。当绝对值 增加时,圆球半径会减小,圆心会靠近原点。当圆心与原点同点时, 达到最大值 。
每一个 -坐标曲面都是不相交的环面。每一个环面都包围着焦圆。环面半径为
- 。
曲线与 z-轴同轴。当 值增加时,圆球面的半径会减少,圆球心会靠近焦点。
逆变换
图 3 )点 P 的坐标
与
的几何诠释。在一个方位角
为常数的平面里,圆环坐标系变成双极坐标系。
与
的夹角
的弧度是
。
与
的比例的
自然对数是
。
与
的等值曲线都是圆圈,分别以红色与蓝色表示。两条等值曲线以直角相交(以洋红色表示)。
是 与 的比例的自然对数:
- 。
圆环坐标 可以用直角坐标 来表达。方位角 的公式为
- 。
点 P 与两个焦点之间的距离是
- 、
- 。
如图 3 , 是两条从点 P 到两个焦点的线段 与 的夹角。这夹角的弧度是 。用余弦定理来计算:
- 。
标度因子
圆环坐标 与 的标度因子相等:
- 。
方位角的标度因子为
- 。
无穷小体积元素是
- 。
拉普拉斯算子是
- 。
其它微分算子,像 、 ,都可以用 坐标表示,只要将标度因子代入在正交坐标系条目内对应的一般公式。












