数学上提及的映射的限制(英:restriction),指对于一个映射,不改变其对应关系而重新取其原定义域的子集为定义域的操作。同种概念可更一般地针对二元关系或多元关系等进行定义。
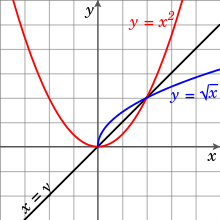
在全体实数组成的集合

上定义的函数

不存在
反函数。但若将其定义域限制到非负实数的集合,则该函数存在反函数,名为

的
算术平方根函数。
由映射  到其定义域的子集
到其定义域的子集  的限制所得的映射可记为
的限制所得的映射可记为  或
或  。
。
定义
设 为从集合 到集合 的映射,即 的定义域为 。对于 的子集 ,映射 到 的限制(又称 对 的限制函数)即为[1]:
通俗而言, 到 的限制可看作虽与原映射相同,但仅在 上被定义的映射。
若设映射 为在笛卡儿积 上的关系 , 到 的限制可以其图像表示:
例子
1. 非单射函数 到 的限制即为单射 。
2. 阶乘函数为伽玛函数到自然数集 的限制。
性质
- 映射 到其定义域 的限制 。
- 某限制函数到其定义域的子集的限制,与其原函数到该集合的限制相同。即若 ,则 成立。
- 集合 上的恒等函数到子集 的限制为从 到 的包含映射[2]。
- 连续函数的限制函数也是连续的[3][4]。
应用
反函数
若某函数存在反函数,其映射必为单射。若映射 非单射,可以限制其定义域以定义其一部分的反函数。如:
因为 ,故非单射。但若将定义域限制到 时该映射为单射,此时有反函数
(若限制定义域至 ,输出 的负平方根的函数为反函数。)另外,若允许反函数为多値函数,则无需限制原函数的定义域。
粘接引理
更多信息:粘接引理
点集拓扑学中的粘接引理联系了函数的连续性与限制函数的连续性。
粘接引理
- 设拓扑空间 的子集 同时为开或闭,且满足 ,设 为拓扑空间。若映射 到 及 的限制都连续,则 也是连续的。
基于此结论,粘接在拓扑空间中的开或闭集合上定义的两个连续函数,可以得到一个新的连续函数。
层
层将函数的限制推广到其他物件的限制。
层论中,拓扑空间 的每个开集 ,有另一个范畴中的物件 与之对应,其中要求 满足某些性质。最重要的性质是,若一个开集包含另一个开集,则对应的两个物件之间有限制态射,即若 ,则有态射 ,且该些态射应仿照函数的限制,满足下列条件:
- 对 的每个开集 ,限制态射 为 上的恒等态射。
- 若有三个开集 ,则复合 。
- (局部性)若 为某个开集 的开覆盖,且 满足:对所有 , ,则 。
- (黏合) 若 为某个开集 的开覆盖,且对每个 ,给定截面 ,使得对任意两个 ,都有 在定义域重叠部分重合(即 ),则存在截面 使得对所有 , 。
所谓拓扑空间 上的层,就是该些物件 和态射 组成的整体 。若仅满足前两项条件,则称为预层。
出处
参考文献
- Stoll, Robert. Sets, Logic and Axiomatic Theories. W. H. Freeman and Company. 1974.
- Halmos, Paul, Naive Set Theory, Princeton, NJ: D. Van Nostrand Company, 1960
- Munkres, James R, Topology 2, Upper Saddle River: Prentice Hall, 2000
- Colin Conrad, Adams; David Franzosa, Robert, Introduction to topology: pure and applied, Pearson Prentice Hall, 2008







