泰博定理
泰博定理原是法国几何学家维克多·泰博(Victor Thébault,1882年-1960年)提出的平面几何问题。
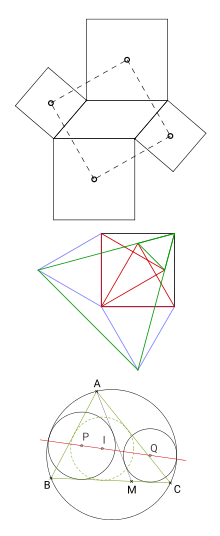
- 取平行四边形的边为正方形的边,作四个正方形(同时在平行四边形内或外皆可)。正方形的中心点所组成的四边形为正方形。(此为凡·奥贝尔定理的特例。)
- 取正方形的两条邻边为三角形的边,作两个等边三角形(同时在正方形内或外皆可)。这两个三角形不在正方形边上的顶点,和正方形四个顶点中唯一一个不是三角形顶点的顶点,组成一等边三角形。
- 给定任意三角形ABC,BC上任意一点M。作两个圆形,均与AM、BC、外接圆相切。该两圆的圆心和三角形内切圆心共线。(应用:日本定理)
第三题是最难的。1938年《美国数学月刊》曾刊出第三题,但直至1973年才为荷兰数学家H. Streefkerk证出。2003年,Ayme发现早在1905年Y. Sawayama已解决这题。
参考
- cut-the-knot (页面存档备份,存于互联网档案馆)
- Ayme, J.-L. "Sawayama and Thebault's Theorem." Forum Geom. 3, 225-229, 2003. (页面存档备份,存于互联网档案馆)