等截共轭
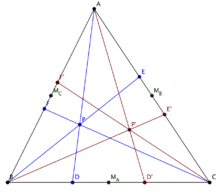
平面几何中,已知三角形ABC,点P不在直线BC、CA、AB上。直线AP、BP、CP与直线BC、CA、AB分别相交于三点D、E、F。边BC、CA、AB的中点分别是MA、MB、MC。分别以此三点为中心,将三点D、E、F点对称到三点D' 、E' 、F' 。则根据塞瓦定理的逆定理,直线AD' 、BE' 、CF' 必然相交于一点P' 。我们将P' 称为P对于三角形ABC的等截共轭。根据定义,P也是P' 对于三角形ABC的等截共轭。
重心G的等截共轭是本身。Gergonne点和奈格尔点等截共轭。
已知P的重心坐标=x : y : z,那么它的等截共轭P' 的重心坐标=1/x : 1/y : 1/z。又P的三线坐标=p : q : r,那么它的等截共轭P' 的三线坐标=1/a2p : 1/b2q : 1/c2r。其中a、b、c是三角形的三边长。
另见
注释和参考
- 埃里克·韦斯坦因. Isotomic Conjugate. MathWorld.