截半 (几何)

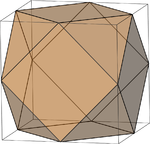
在几何学中，截半（英语：Rectification）是一种将多边形、多面体、密铺、镶嵌或更高维的多胞体从每个边的中点开始切去顶点的一种多面体变换[1]，换句话说，就是截角变换的一种特例，即截角截至中点[2]。所得到的多面体将以截面与多面体原本的面为界。考克斯特符号与施莱夫利符号将截半变换记为r，例如r{4,3}，而康威记号则将截半变换记为a[3][4]，例如aC，r{4,3}与aC皆代表一个截半立方体[5]。

一个截半的立方体（截半立方体）。

康威将截半变换称为ambo[6]。在图论算法中，截半称为内侧图（英语：Medial graph）。

参见

参考文献

  1. ^ Weisstein, Eric W. (编). Rectification. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  2. ^ Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition,  
  3. ^ Weisstein, Eric W. (编). Conway Polyhedron Notation. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  4. ^ Weisstein, Eric W. (编), Cuboctahedron, (Archimedean solid), at MathWorld--A Wolfram Web Resource,Wolfram Research, Inc. （英语） 
  5. ^ Conway, 2008, p288 table
  • Norman Johnson Uniform Polytopes, Manuscript (1991)
    • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, 编辑
    多面体变换
    [ ]
    原像 截角 截半 过截角 对偶 扩展（英语：Expansion (geometry)） 全截（英语：Omnitruncation） 交错
    半变换 扭棱
                                                               
                       
    t0{p,q}
    {p,q}     		t01{p,q}（英语：Truncated polyhedron）
    t{p,q}     		t1{p,q}
    r{p,q}     		t12{p,q}（英语：Bitruncated polyhedron）
    2t{p,q}     		t2{p,q}
    2r{p,q}     		t02{p,q}（英语：Cantellated polyhedron）
    rr{p,q}     		t012{p,q}（英语：Omnitruncated polyhedron）
    tr{p,q}     		ht0{p,q}
    h{q,p}     		ht12{p,q}（英语：Snub polyhedron）
    s{q,p}     		ht012{p,q}（英语：Snub polyhedron）
    sr{p,q}