主验证
验证此公式,可透过因式分解,首先设以下公式:
-
然后代入:
-
透过因式分解,可得:
-
-
这样便可验证:
和立方验证
透过和立方可验证立方和的原理:
-
-
那即是只要减去 及 便可得到立方和,可设:
-
- 右边的方程
运用因式分解的方法:
-
-
-
-
这样便可验证出:
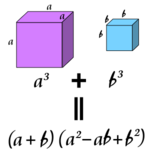
几何验证
图象化
透过绘立体的图像,也可验证立方和。[2]
根据右图,设两个立方,总和为:
-
把两个立方体对角贴在一起,根据虚线,可间接得到:
-
要得到 ,可使用 的空白位置。该空白位置可分割为3个部分:
-
-
-
把三个部分加在一起,便得:
-
-
之后,把 减去它,便得:
上公式发现两个数项皆有一个公因子,把它抽出,并得:
-
可透过和平方公式,得到:
-
-
这样便可证明
反验证
透过 也可反验证立方和。
-
-
-
-
以上计算方法亦可简化为一个表格:
| x)
|
|
|
|
|---|
|
|
|
|
|
|---|
|
|
|
|
|
|---|
这样便可证明