不稳定性
在许多领域中,不稳定是指一个可由其输出或内在状态描述的系统,其状态可能会不受限制的成长[1](有时会称为发散)。另一个对应的词是稳定性理论,稳定有许多种定义,其中一种定义是指对系统施加一个小型的外扰,使系统离开一平衡状态,外扰去除后,系统会回到原来的平衡状态。
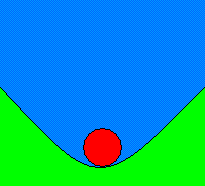
以右图为例:
- 一个山丘上的球,若推往任何一个方向,球会移动离开山丘,在推力消除后,球仍会继续往下滚,离山丘的距离越来越远,这是不稳定的系统。
- 一个山谷中的球,若推往任何一个方向,球会移动离开山谷,但推力消除后,球会回到山谷的位置,这是稳定的系统。
系统除了稳定及不稳定,也可能处于其他的情形,例如系统不会发散也不会回到原平衡状态的临界稳定(例如一个平地上的球),或是其状态会形成某种特定循环的极限环。
在结构工程中,一个结构若承受了过重的负荷,结构就会不稳定。负荷若超过一定的上限,结构的变形会使应力变大,结构 会再进一步的变形,会产生挫曲或局部破坏,这类的研究称为结构稳定性。
大气不稳定性是地球上所有气象系统的重要特性之一。
控制理论中的不稳定性
控制理论中的稳定性有几种不同的定义,最常见的是有界输入有界输出稳定性,有一个系统在有限大小的输入(有界输入)时都有有限大小的输出(有界输出),系统即为稳定。
若一个线性时不变系统其特征方程有实部大于零的根,或有实部为零的重根,此系统即为不稳定系统,这也相当于其状态矩阵有特征值的实部大于零。
固体力学中的不稳定性
- 挫曲:细长物体在受到较大压力时,会因受力而弯曲,因此物体会在应力到达强度之前就因变形而损坏。
- Drucker稳定性:一些应力及应变之间的非线性关系。
- Biot不稳定性(Biot instability):弹性体的表面起皱
- Baroclinic不稳定性[2]。
流体不稳定性
流体不稳定性会出现在液态、气态及等离子态。在流体动力学及磁流动力学中会研究不稳定性,流体不稳定性会包括以下的几种:
- 磁层中出现的气球不稳定性(类似瑞利-泰勒不稳定性)
- 大气不稳定性
- 流体动力不稳定性(大气动力学)
- 惯性不稳定性(Inertial instability)、开尔文-亥姆霍兹不稳定性、对称不稳定性(symmetric instability)、条件性对称不稳定性(conditional symmetric instability)或对流对称不稳定性(convective symmetric instability)、正压不稳定性(barotropic instability)、旋转不稳定性(rotational instability)
- 流体静力不稳定性或热力学不稳定性 (大气热力学)
- 条件不稳定性(Conditional instability)或静不稳定性(static instability)、浮力不稳定性(buoyant instability)、对流不稳定性、绝对不稳定性(absolute instability)
- 流体动力不稳定性(大气动力学)
- 瑞利-贝纳对流
- 漂移磁镜模不稳定性(Drift mirror instability)
- 布鲁托─雷利不稳定性(类似等离子体的Diocotron不稳定性,但不一样)
- 瑞利-泰勒不稳定性
- 普拉托-瑞利不稳定性(类似瑞利-泰勒不稳定性)
- 里克特迈耶-梅什科夫不稳定性(类似瑞利-泰勒不稳定性)
- 激波不稳定性
等离子体不稳定性
等离子体的不稳定性可以分为流体动力的不稳定性以及动力学的不稳定性,也可以区分为其他的分类,例如依azimuthal波数分类。
恒星系统的不稳定性
若一星系或星团其重力位的扰动会造成密度改变,再增强重力位的扰动,此星系或星团即为不稳定的。这类的不稳定性需要和恒星的移动相当相关,因此扰动不会被随机运动所淡化。若系统出现不稳定性后,系统一般会比原来更“热”(随机性更高),恒星系统的稳定性有:
- 快速旋转圆盘的棒状不稳定性。
- 金斯不稳定性:恒星形成时,当分子云的热压力不足以抵抗引力时,会在引力的作用下发生坍缩。
- 水龙软管不稳定性[4]。
- 重力热力学不稳定性(Gravothermal instability)
- 径向轨道不稳定性(Radial-orbit instability)
- 冷旋转圆盘的各种不稳定性。
关节不稳定性
关节不稳定是身体扭伤后最常见的后遗症。力学性的不稳定包括不足的稳定结构以及超过肢体限制的活动性。机能性的不稳定包括受伤关节反复的扭伤[5]。受伤导致肌肉运动知觉的缺陷及受损的关节姿势控制。肌肉无力、潜在不稳定、姿势控制能力减退的人比平常人更容易受伤。不稳定性会导致重心摆动(postural sway)的增加,量测方式是量测个人偏离理想压力中心的时间及距离。压力中心的定义是重心对地的投影位置。研究者有提出理论,若关节受伤有导致传入神经阻滞、感觉神经纤维的中断、及机能上的不稳定,会影响其重心摆动[6]。关节的稳定性可以用外部支持系统或是调整肢体的力学来改善,支架提供的力学支撑可以维持姿势控制,并且增加稳定性。
相关条目
- 等离子体不稳定性
- 稳定-不稳定悖论
- 失败国家:政治的不稳定性
- 不稳定对超新星
- 白克兰电流
参考资料
- ^ 存档副本. [2015-03-09]. (原始内容存档于2021-08-07).
- ^ 存档副本. [2015-03-09]. (原始内容存档于2021-08-07).
- ^ Shengtai Li, Hui Li. Parallel AMR Code for Compressible MHD or HD Equations. Los Alamos National Laboratory. [2015-03-10]. (原始内容存档于2016-03-03).
- ^ Merritt, D.; Sellwood, J., Bending Instabilities of Stellar Systems, The Astrophysical Journal, 1994, 425: 551–567, Bibcode:1994ApJ...425..551M, doi:10.1086/174005
- ^ Guskiewicz, K. M.; Perrin, David H. Effect of Orthotics on Postural Sway Following Inversion Ankle Sprain. Journal of Orthopedic and Sports Physical Therapy. 1996, 23 (5): 326–331. doi:10.2519/jospt.1996.23.5.326.
- ^ Pintsaar, A.; Brynhildsen, J.; Tropp, H. Postural Corrections after Standardised Perturbations of Single Limb Stance: Effect of Training and Orthotic Devices in Patients with Ankle Instability. British Journal of Sports Medicine. 1996, 30 (2): 151–155 [15 October 2013]. doi:10.1136/bjsm.30.2.151.