奇点 (几何)

平面上的代数曲线可以定义为满足方程f(x, y)=0的点的集合，其中f是多项式函数。

若f展开为以下的形式

${\displaystyle f=a_{0}+b_{0}x+b_{1}y+c_{0}x^{2}+2c_{1}xy+c_{2}y^{2}+\dots \,}$ 

且若原点(0, 0)在曲线上，则a₀=0。若b₁≠0，则隐函数定理可确定有一光滑函数h，使得在原点附近y=h(x)会成立。同様的，若b₀≠0，则在原点附近曲线会接近x=k(y) 。上述任何一个情形下，都有一个光滑映射从R映射到原点附近曲线所在的平面，注意在原点处

${\displaystyle b_{0}={\partial f \over \partial x},\,b_{1}={\partial f \over \partial y},}$ 

因此只要任何一个f的偏导数不为零，曲线即为非奇异。曲线的奇点出现在二个偏导数皆为零的位置。

${\displaystyle f(x,y)={\partial f \over \partial x}={\partial f \over \partial y}=0.}$ 

非奇点

假设曲线通过原点，原点附近可近似为y=mx，则f可以写为如下的式子

${\displaystyle f=(b_{0}+mb_{1})x+(c_{0}+2mc_{1}+c_{2}m^{2})x^{2}+\dots .\,}$ 

若b₀+mb₁不为零，则f=0在x=0处有阶数为1的解。若b₀+mb₁=0 ，则f=0在x=0处有阶数为2（或更高）的解，且y=mx及b₀x+b₁y=0都会是曲线的切线。此时，若if c₀+2mc₁+c₂m²不为零，则曲线在和y=mx接触处有二重点（point of double）。若x², c₀+2mc₁+c₂m²的系数为零，但x³系数不为零，则原点是曲线的拐点。若x²和x³的系数都是零，则原点称为曲线的波动点（point of undulation）。上述分析可以应用在曲线上的任意点，只要平移坐标轴，使要分析的点变成原点即可^[1]。

二重点

若在上述说明中，b₀和b₁都是零，但至少c₀、c₁和c₂中有一个不为零，则原点即为曲线的二重点。再令y=mx，则f可写成

${\displaystyle f=(c_{0}+2mc_{1}+c_{2}m^{2})x^{2}+(d_{0}+3md_{1}+3m^{2}d_{2}+d_{3}m^{3})x^{3}+\dots .\,}$ 

二重点可以依以下方程的解来分类： c₀+2mc₁+m²c₂=0.

叉点

若c₀+2mc₁+m²c₂=0有二个m的实根，也就是c₀c₂−c₁²<0，则原点为叉点。曲线在叉点和自身相交，二条切线对应c₀+2mc₁+m²c₂=0的二个解。原点为函数f的鞍点。

孤立点

若c₀+2mc₁+m²c₂=0没有m的实根，也就是c₀c₂−c₁²>0，则原点为孤立点。在实数平面上，原点为曲线的一个孤点，不过若当做复数曲线来考虑，c₀+2mc₁+m²c₂=0的二部分的解之间有复数的切线相连。此情形下函数在原点处有极值。

尖点

若c₀+2mc₁+m²c₂=0有一个m的二重根，也就是c₀c₂−c₁²=0，原点称为尖点。此时曲线在原点变动方向，产生一个尖锐的图形。曲线在原点处有单一的切线，但是可视为二条恰好重合的切线。

进一步的分类

node一词是用来表示叉点或是孤立点，也就是不为尖点的二重点。曲线中node数量及尖点数量是二个曲线的不变量，在普吕克公式（英语：Plücker formula）中有用到。

若c₀+2mc₁+m²c₂=0的一个解也是d₀+3md₁+3m²d₂+m³d₃=0的解，则曲线对应的分支在原点为拐点，此时原点称为flecnode。若两条切线都有此性质，则c₀+2mc₁+m²c₂为d₀+3md₁+3m²d₂+m³d₃的因式，原点称为biflecnode^[2]。

三重点

若f中所有小于k次方的系数都为零，且至少有一项k次方的系数不为0，此曲线即有k阶的多重点。一般而言曲线在原点处有k条切线，不过有些切线可能会是虚数^[3]。

R²平面中的参数曲线定义为由R→R²函数 g的像，函数g(t) = (g₁(t),g₂(t))。其中的奇点为满足以下条件的点

${\displaystyle {dg_{1} \over dt}={dg_{2} \over dt}=0.}$ 

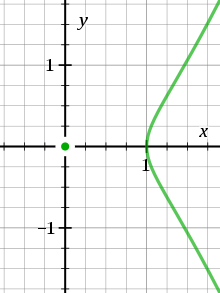
许多曲线可以用方程式来定义，也可以用参数方程定义。代数曲线x³−y² = 0会有一尖点，若改用参数式g(t) = (t²,t³)，尖点仍然存在。

不过有时奇点的数量可能会随定义方式而不同。例如y²−x³−x² = 0在原点有一奇点，为叉点，但若用参数式g(t) = (t²−1,t(t²−1))，因为g′(t) 在任意位置都不为零，因此同一曲线的参数式中，不存在奇点。

在将曲线用参数方程表示时，参数的选择会影响一些相关的分析。例如直线y = 0，本身不存在奇点，若用参数方程g(t) = (t,0)，也没有奇，但若用参数方程g(t) = (t³,0)表示，在原点处就会有一个奇点。因此参数式奇点的专业用语应该称为光滑映射的奇点（singular points of a smooth mapping）比较合适。

哈斯勒·惠特尼有一定理提到^[4][5]

任意Rⁿ内的闭集都可以表示为某一光滑函数f:Rⁿ→R，其方程f⁻¹(0)的解集合。

上述的定义可以延伸到用隐函数定义的曲线，定义方式为f⁻¹(0)的解集合，而f为光滑函数，因此不一定只考虑代数簇，可以延伸到更高维度的曲线。

任何参数化的曲线可以定义为隐函数的曲线，曲线奇点的分类也会在代数簇上的奇点（英语：singular point of an algebraic variety）的分类中加以研究。

以下是一些可能的奇点：

• 单独的一个点：x²+y² = 0，属于孤立点
• 二条线交于一点：x²−y² = 0，属于叉点
• 尖点：x³−y² = 0
• rhamphoid尖点：x⁵−y² = 0.