Β分布,亦称贝它分布、Beta 分布(Beta distribution),在概率论中,是指一组定义在 区间的连续概率分布,有两个母数
区间的连续概率分布,有两个母数 。
。
Β分布|
概率密度函数 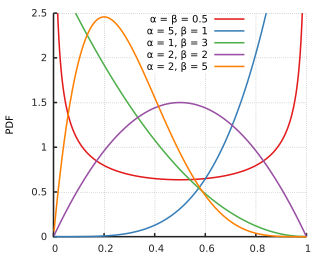 |
|
累积分布函数 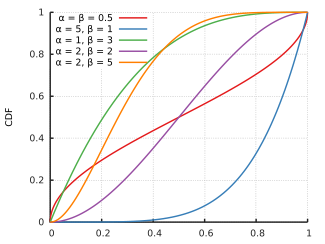 |
| 参数 |

 |
|---|
| 值域 |
 |
|---|
| 概率密度函数 |
 |
|---|
| 累积分布函数 |
 |
|---|
| 期望值 |
![\operatorname {E}[x]={\frac {\alpha }{\alpha +\beta }}\!](/media/math_img/1245/0569ee58528ca526f9cdab57675a2d0d73bf4766.svg)
![\operatorname {E}[\ln x]=\psi (\alpha )-\psi (\alpha +\beta )\!](/media/math_img/1245/73a2d06fc2308f395e3dbaed6bb7d0b975d38eb1.svg)
(见双伽玛函数) |
|---|
| 中位数 |
 无解析表达 无解析表达 |
|---|
| 众数 |
 for for  |
|---|
| 方差 |
 |
|---|
| 偏度 |
 |
|---|
| 峰度 |
见文字 |
|---|
| 熵 |
见文字 |
|---|
| 矩生成函数 |
 |
|---|
| 特征函数 |
 (见合流超几何函数) (见合流超几何函数) |
|---|
定义
概率密度函数
Β分布的概率密度函数是:
-
其中 是Γ函数。随机变量X服从参数为 的Β分布通常写作
-
累积分布函数
Β分布的累积分布函数是:
-
其中 是不完全Β函数, 是正则不完全贝塔函数。
性质
参数为 Β分布的众数是:
- [1]
期望值和方差分别是:
-
-
偏度是:
-
峰度是:
-
或:
-
阶矩是:
-
其中 表示递进阶乘幂。 阶矩还可以递归地表示为:
-
另外,
-
给定两个Β分布随机变量, X ~ Beta(α, β) and Y ~ Beta(α', β'), X的微分熵为:[2]
-
其中 表示双伽玛函数。
联合熵为:
-
其KL散度为:
-
参见
外部链接
参考文献
- ^ Johnson, Norman L., Samuel Kotz, and N. Balakrishnan (1995). "Continuous Univariate Distributions, Vol. 2", Wiley, ISBN 978-0-471-58494-0.
- ^ A. C. G. Verdugo Lazo and P. N. Rathie. "On the entropy of continuous probability distributions," IEEE Trans. Inf. Theory, IT-24:120–122,1978.









![\operatorname {E}[x]={\frac {\alpha }{\alpha +\beta }}\!](/media/math_img/1245/0569ee58528ca526f9cdab57675a2d0d73bf4766.svg)
![\operatorname {E}[\ln x]=\psi (\alpha )-\psi (\alpha +\beta )\!](/media/math_img/1245/73a2d06fc2308f395e3dbaed6bb7d0b975d38eb1.svg)






