四维十二胞体
在四维空间中没有正十二胞体,但有四种柱体柱 :三角九角柱体柱 四角八角柱体柱 五角七角柱体柱 六角六角柱体柱 [1] 六角柱 不是正图形 ,因此不能算是正十二胞体。
名称
考克斯特
胞
图像
展开图
三角九角柱体柱
3个九角柱 三角柱
四角八角柱体柱
4个八角柱
五角七角柱体柱
5个七角柱
六角六角柱体柱
12个六角柱
五维十二胞体
在五维空间中,十二胞体由12个四维多胞体组成,虽然没有正十二胞体,但存在许多半正多胞体,例如四种经过一次康威变换 的半正多胞体[2]
六维十二胞体
在六维空间中,十二胞体为由12个五维多胞体所组成的多胞体,而由十二个五维超正方体 六维超立方体
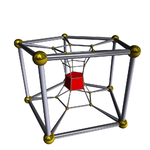
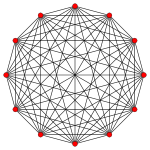
十一维正十二胞体
正十二胞体 类型 正十一维多胞体 家族 单纯形 维度 十一维 对偶多胞形 十一维正十二胞体 (自身对偶 ) 数学表示法 考克斯特符号 施莱夫利符号 {3,3,3,3,3,3,3,3,3,3}10 } 性质 十维胞 12个十维正十一胞体 九维胞 66个九维正十胞体 八维胞 220个八维正九胞体 七维胞 495个七维正八胞体 六维胞 792个六维正七胞体 五维胞 924个五维正六胞体 四维胞 792个正五胞体 胞 495个正四面体 面 220个正三角形 边 66 顶点 12 欧拉示性数 2 特殊面或截面 皮特里多边形 正十二边形 组成与布局 顶点图 十维正十一胞体 对称性 对称群 A11 [3,3,3,3,3,3,3,3,3,3]
在十一维空间几何学中,十一维正十二胞体 (Dodecadakon 或Dodeca-11-tope )又称为11-单纯形 (11-simplex )是十一维空间的一种自身对偶的正多胞体,由12个十维正十一胞体 组成,是一个十一维空间中的单纯形[3] [4]
性质 四维正十二胞体共有12个维面、66个维轴和220个维端,其各维度的的胞数分别为12个十维胞、66个九维胞、220个八维胞、495个七维胞、792个六维胞、924个五维胞、792个四维胞、495个三维胞、220个面、66条边和12个顶点 ,其二面角 为cos−1 (1/11)大约是84.78°[5] [6] [7]
顶点坐标 边长为2且几何中心 位于原点的十一维正十二胞体的顶点坐标会落在:
(
1
/
66
,
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
1
/
10
,
1
/
6
,
1
/
3
,
±
1
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)}
(
1
/
66
,
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
1
/
10
,
1
/
6
,
−
2
1
/
3
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)}
(
1
/
66
,
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
1
/
10
,
−
3
/
2
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)}
(
1
/
66
,
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
1
/
15
,
−
2
2
/
5
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)}
(
1
/
66
,
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
1
/
21
,
−
5
/
3
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
66
,
1
/
55
,
1
/
45
,
1
/
6
,
1
/
28
,
−
12
/
7
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
66
,
1
/
55
,
1
/
45
,
1
/
6
,
−
7
/
4
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ -{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
66
,
1
/
55
,
1
/
45
,
−
4
/
3
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ {\sqrt {1/45}},\ -4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
66
,
1
/
55
,
−
3
1
/
5
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ {\sqrt {1/55}},\ -3{\sqrt {1/5}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
1
/
66
,
−
20
/
11
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left({\sqrt {1/66}},\ -{\sqrt {20/11}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
(
−
11
/
6
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
{\displaystyle \left(-{\sqrt {11/6}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}
参见 参考文献
^ Olshevsky, George, Duoprism Glossary for Hyperspace .
^ Kaleidoscopes: Selected Writings of H.S.M. Coxeter , edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, 互联网档案馆 )^ Coxeter , Regular Polytopes , (3rd edition, 1973), Dover edition, John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1 )^ (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
^ (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
^ (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]