十五面体
| 部分的十五面体 | |
|---|---|
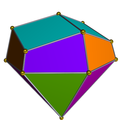 三角帐塔柱的对偶 |
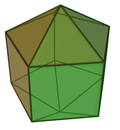 双五角锥柱 |
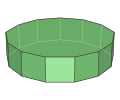 正十三角柱 |
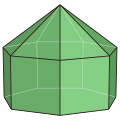 七角锥柱 |
在几何学中,十五面体是指具有15个面的多面体。在十五面体当中没有任何一个形状是正多面体,换言之即正十五面体并不存在,十五面体亦无法填充空间,换言之即空间填充十五面体并不存在[1]:88。虽然正十五面体不存在,但仍有存在一些等面或等角的十五面体,亦有一些十五面体皆由正多边形组成,例如十三角柱和双五角锥柱。
凸十五面体
所有十五面体中一共有23,833,988,129个拓扑不同构的凸十五面体,不包括镜像,并且至少需要包含10个顶点[5](如果两个多面体具有本质上不同的面排列、边与顶点的相接方式,则它们是“拓扑不同构”,因为如果两个立体间有不同的面排列、边与顶点的相接方式,则就无法仅透过改变边的长度或边或面之间的角度来将一个多面体形变成另一个)。
常见的十五面体
十三角柱
十三角柱是一种底面为十三边形的柱体,是十五面体的一种,其由15个面、26个顶点和39个边组成。正十三角柱代表每个面都是正多边形的十三角柱,其每个顶点都是2个正方形和1个十三边形的公共顶点,顶点图以 表示,在施莱夫利符号中可以利用{13}×{} 或 t{2, 13}来表示;在考克斯特—迪肯符号中可以利用 来表示;在威佐夫符号中可以利用2 13 | 2来表示;在康威多面体表示法中可以利用P13来表示。若一个正十三角柱底边的边长为 、高为 ,则其体积 和表面积 为[6]:
十四角锥
十四角锥是一种底面为十四边形的锥体,是十五面体的一种,其具有15个面、28条边和15个顶点,其对偶多面体是自己本身[7]。正十四角锥是一种底面为正十四边形的十四角锥。若一个正十四角锥底边的边长为 、高为 ,则其体积 和表面积 为[7]:
詹森多面体
| 双五角锥柱 |
詹森多面体对偶
部分詹森多面体具有15个顶点[9],因此其对偶多面体为十五面体,这些立体有正五角帐塔的对偶、正三角帐塔柱的对偶、三侧锥六角柱的对偶、侧帐塔截角四面体的对偶等多面体。
| 正五角帐塔 |
三角帐塔柱 |
正三角帐塔反角柱 |
| 正五角帐塔的对偶 (十五面体) |
三角帐塔柱的对偶 (十五面体) |
正三角帐塔反角柱的对偶 (十五面体) |
十五面体列表
| 名称 | 种类 | 图像 | 符号 | 顶点 | 边 | 面 | χ | 面的种类 | 对称性 | 展开图 |
|---|---|---|---|---|---|---|---|---|---|---|
| 十三角柱 | 棱柱体 | t{2,13} {13}x{} |
26 | 39 | 15 | 2 | 2个十三边形 13个矩形 |
D13h, [13,2], (*13 2 2) | ||
| 十四角锥 | 棱锥体 | ( )∨{14} | 15 | 28 | 15 | 2 | 1个十四边形 14个三角形 |
C14v, [14], (*14 14) | ||
| 七角锥柱 | 角锥柱 | 15 | 28 | 15 | 2 | 7个三角形 7个矩形 1个七边形 |
D7h, [7,2], (*227), order 28 | |||
| 七角锥台锥 | 截角双锥 | 15 | 28 | 15 | 2 | 7个三角形 7个梯形 1个七边形 |
D7h, [7,2], (*227), order 28 | |||
| 双五角锥柱 | 双角锥柱 詹森多面体 |
12 | 25 | 15 | 2 | 10个三角形 5个正方形 |
D5h, [5,2], (*225) | |||
| 正五角帐塔的对偶 | 詹森多面体的对偶 | 12 | 25 | 15 | 2 | 10个三角形 5个筝形 |
D5h, [5,2], (*225) | |||
| 三角帐塔柱的对偶 | 詹森多面体的对偶 | 14 | 27 | 15 | 2 | 6个等腰三角形 9个四边形 |
C3v | |||
| 正三角帐塔反角柱的对偶 | 詹森多面体的对偶 | 16 | 33 | 15 | 2 | 6个五边形 3个四边形 6个筝形 |
C3v |
参考资料
- ^ 帕克麦特. 數學大觀念2:從掐指一算到穿越四次元的數學魔術. 猫头鹰书房. Mao tou ying chu ban. 2020. ISBN 9789862624265.
- ^ Montejano, JM and Rodríguez, JL and Gutierrez-Wing, C and Miki, M and José-Yacamán, M. Crystallography and Shape of Nanoparticles and Clusters (PDF). Encyclopedia of Nanoscience and Nanotechnology X. 2004: 1–44.
- ^ Lagunov, VA and Sinani, AB. Formation of a bistructure of a solid in a computer experiment. Physics of the Solid State (Springer). 1998, 40 (10): 1742–1747. doi:10.1134/1.1130648.
- ^ CN patent 201280830Y,卓新 & 吴建挺,“等十五面体帐篷结构”,发表于2009-07-29,指定于浙江大学和浙江展诚建设集团股份有限公司
- ^ Counting polyhedra. numericana.com.
- ^ Wolfram, Stephen. "Tridecagonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ 7.0 7.1 Wolfram, Stephen. "Tetradecagon pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Johnson, Norman W. Convex Solids with Regular Faces. Canadian Journal of Mathematics. 1966, 18: 169–200. ISSN 0008-414X. Zbl 0132.14603. doi:10.4153/cjm-1966-021-8.
- ^ Gagnon, Sylvain. Les polyèdres convexes aux faces régulières [Convex polyhedra with regular faces] (PDF). Structural Topology. 1982, (6): 83–95.