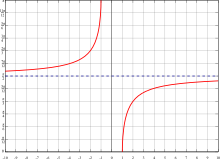
反正割
 | |
| 性质 | |
| 奇偶性 | 非奇非偶 |
| 定义域 | [1] |
| 到达域 | |
| 周期 | N/A |
| 特定值 | |
| 当x=0 | 不存在[注 1] |
| 当x=+∞ | (90°) |
| 当x=-∞ | (90°) |
| 当x=1 | 0 |
| 当x=-1 | (180°) |
| 其他性质 | |
| 渐近线 | (y=90°) |
反正割(英语:arcsecant[3]、记为:或)是一种反三角函数[4],对应的三角函数为正割函数,用来计算已知斜边与邻边的比值求出其夹角大小的函数,是高等数学中的一种基本特殊函数,其输入值与反余弦互为倒数。
由于正割函数在实数上不具有一一对应的关系,所以不存在反函数,但我们可以限制其定义域,因此,反正割是单射也是可逆的,由于限制正割函数的定义域在([0, 180°])时,其值域是全体实数,但在区间不存在。
符号
反正割一般记为 [5]或 [6][7][8][9],以表示正割的反函数。也有以大写书写的版本Arcsec z[10]和Sec-1 z一般用于表示多值函数[6]。在符号 上的上标-1是表示反函数,而不是乘法逆元素。但根据ISO 31-11应将反正切函数记为 ,因为 可能会与 混淆, 是余弦函数。
定义
原始的定义是将正割函数限制在 ([0, 180°])的反函数
在复变分析中,反正割是这样定义的:
这个动作使反正割被推广到复数。
下图表示推广到复数的反正割复数平面函数图形,可以见到图中央有一条明显的横线正好是实数中未被定义的区间[-1,1]。
直角三角形中
在直角三角形中,反正割定义为已知斜边c与邻边b比值对应的 的大小,也就是:
此外在直角三角形中,若已知斜边为 且邻边为单位长, 代入反正割可求得对应的角的大小:
因此,根据毕氏定理可以使反正割利用其他反三角函数表示:
直角坐标系中
若 是平面直角坐标系xOy中的一个未知的象限角, 是角的终边上一点, 是P到原点O的距离,若已知 ,则可利用反正割求得未知的象限角 :
级数定义
反正割函数可以使用无穷级数定义:
反正割函数的泰勒展开式为:
参见
注释
参考文献
- ^ Weisstein, Eric W. "Inverse Secant." From MathWorld--A Wolfram Web Resource.
- ^ 反正割在x=0的极限 wolframalpha.com [2014-08-08]
- ^ 反正割arcsecant-学术名词资讯 (页面存档备份,存于互联网档案馆) 国家教育研究院 terms.naer.edu.tw [2014-08-07]
- ^ Gradshtein, I. S., I. M. Ryzhik, et al. (2000). Table of integrals, series, and products, Academic Pr.
- ^ Zwillinger, D.(Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.
- ^ 6.0 6.1 Abramowitz, M. and Stegun, I. A.(Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing (页面存档备份,存于互联网档案馆). New York: Dover, pp. 79-83, 1972.
- ^ Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science (页面存档备份,存于互联网档案馆). New York: Springer-Verlag, p. 315, 1998.
- ^ Jeffrey, A. Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, 2000.
- ^ 《 Exponentielle & logarithme 》, § Fonctions circulaires réciproques, Dictionnaire de mathématiques – algèbre, analyse, géométrie, Encyclopædia Universalis.
- ^ Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 141-143, 1987.
外部链接
- 埃里克·韦斯坦因. Inverse Secant. MathWorld.
- 埃里克·韦斯坦因. Arcsecant. MathWorld.








![[0,\pi ]](/media/math_img/2102/3e2a912eda6ef1afe46a81b518fe9da64a832751.svg)
![[-1,1]](/media/math_img/2102/51e3b7f14a6f70e614728c583409a0b9a8b9de01.svg)