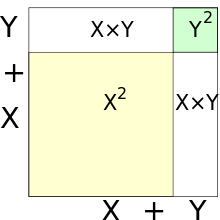
中一新生之梦
Freshman's dream(中文可译“新手之梦”)指的是错误方程式“ = ”,当中 是一个实数(通常是大于1的正整数)。初阶学生经常误以为括号外的次方可以直接分配给括号内的项[1][2]。其实只要假设 就可以简单发现方程式并不成立:透过乘法分配律,。至于 值更大的方程式,则可以使用二项式定理计算正确答案。
在热带几何的世界,加法取代了乘法,而极值取代了加法。在此情况下,“Freshman's dream”便是正确[3]。
“Freshman's dream”也可代指另一项定理,,当中 是质数,而 和 是在具有 特征的交换环上的代数。由于 能够整除首项和末项以外的二项式系数,使中间的所有项都等于零,所以这个“错误”实际上可以做到正确答案[4]。
历史与别名
1940年一篇有关模曲线的文章中,桑德斯·麦克兰恩引用斯蒂芬·科尔·克莱尼指出,体的特征2“ ”有可能破坏中一新生的代数观念。言论是可追溯的最早将“中一新生”与体的正数特征[5],自此大部分代数课本都提及这个惯常误解,其中1974年汤马士·亨嘉福的代数课本似乎是首次使用“Freshman's dream”一词[6]。别名包括1998年庄·法黎课本中的“Freshman exponentiation”(中文可译“中一新生之幂”)[7];又鉴于 可透过二项式定理计算,因而又被称为“小孩的二项式定理”(Child's binomial theorem)[8]或“中学生的二项式定理”(Schoolboy binomial theorem)[9]。
例子
- ,但 .
- (即 )在大多数情况下都不等于 。例如: ,而 。
质数定理
当 是质数,而 和 是在具有 特征的交换环上的代数,那么 。此理论可透过研究二项式系数的质数因数而论证:
第 n 个二项式系数为 。
由于分子是 的阶乘,所以可以被 整除。不过当 之时, 和 都少于 ,因而两者都不能被整除。但二项式系数必然是整数,因此第 n 个二项式系数可被 整除,交换环继而等于零。自此整条方程式只剩下第0个和第 p 个二项式系数,因此可证 。结果也证明 p 次方制造了自同态,又称交换环的弗罗贝尼乌斯自同态[8]。
在此方程中, 必须是质数才可成立。有一相类近的定理指出,当 是质数的话,在 多项式环中, 。此定理成为现代质数测试中的关键[8]。
参见
参考文献
- ^ Julio R. Bastida, Field Extensions and Galois Theory, Addison-Wesley Publishing Company, 1984, p.8.
- ^ Fraleigh, John B., A First Course in Abstract Algebra, Addison-Wesley Publishing Company, 1993, p.453, ISBN 0-201-53467-3.
- ^ Difusión DM, Introduction to Tropical Algebraic Geometry (1 of 5), 2018-02-23 [2019-06-11], (原始内容存档于2020-06-17)
- ^ How is (x+y)p≡xp+yp mod p for any prime number p. Mathematics Stack Exchange. [2020-08-12]. (原始内容存档于2022-03-25).
- ^ Colin R. Fletcher, Review of Selected papers on algebra, edited by Susan Montgomery, Elizabeth W. Ralston and others. Pp xv, 537. 1977. ISBN 0-88385-203-9 (Mathematical Association of America), The Mathematical Gazette, Vol. 62, No. 421 (Oct., 1978), The Mathematical Association. p. 221.
- ^ Thomas W. Hungerford, Algebra, Springer, 1974, p. 121; also in Abstract Algebra: An Introduction, 2nd edition. Brooks Cole, July 12, 1996, p. 366.
- ^ John B. Fraleigh, A First Course In Abstract Algebra, 6th edition, Addison-Wesley, 1998. pp. 262 and 438.
- ^ 8.0 8.1 8.2 Granville, Andrew. It Is Easy To Determine Whether A Given Integer Is Prime (PDF). BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY: 3–38. 2004-09-30 [2020-08-12]. (原始内容存档 (PDF)于2008-05-14).
|volume=被忽略 (帮助) - ^ EGMO Training 2017 - Exponents (mod p) (PDF). (原始内容存档 (PDF)于2017-11-19).
- ^ 1800–1900 Search for "freshman's dream". Google books. [2020-08-12]. (原始内容存档于2022-02-08).
- ^ Bentley's miscellany 26. 1849: 176.