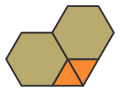
六角化截角三角形镶嵌

在几何学中，六角化截角三角形镶嵌是一种平面密铺，由正三角形和正六边形组成。该镶嵌属于复合正多边形密铺[2]，是一种不均匀半正镶嵌图，并且是Krötenheerdt提出的较有系统的14种不均匀半正镶嵌图之一。[3][4]

六角化截角三角形镶嵌
六角化截角三角形镶嵌
类别Demiregular Tessellation
对偶多面体六边形-梯形镶嵌
数学表示法
施莱夫利符号kt{3,6}
威佐夫符号
（英语：Wythoff symbol）		2 6 | 3
组成与布局
面的种类正三角形
正六边形
顶点图(1/7)(36) + (6/7)(32,62)[1]
对称性
对称群
  • 632, (p6m), [6,3]
旋转对称群
（英语：Rotation_groups）		p6, [6,3]+, (632)
图像
Regular polygons meeting at vertex 4 3 3 6 6.svgRegular polygons meeting at vertex 6 3 3 3 3 3 3.svg
(1/7)(36) + (6/7)(32,62)[1]
（顶点图）
Kleetope hexagonal tiling ktH dual.png
六边形-梯形镶嵌
（对偶多面体）

结构

六角化截角三角形镶嵌表示一个截去所有顶点的三角形镶嵌，将截完顶点后的六边形面从重心分割出六个正三角形所得到的图形。其结构类似于六角化六边形镶嵌，但其六角化花式是从六边形镶嵌第二种一阶半正表面涂色（如下图）的第二种表面涂色（即图中红色）进行六角化之几何图形。

 

对偶镶嵌

此镶嵌的对偶镶嵌也可以视为梯形与六边形组合而成的镶嵌，因此又称为六边形-梯形镶嵌。

 

相关多面体与镶嵌

与六角化截角三角形镶嵌相似的镶嵌有三角形镶嵌与六角化六边形镶嵌。

全部六角化 六角化六边形镶嵌 六角化截角三角形镶嵌
     
正三角形镶嵌家族的半正镶嵌
对称性: [6,3], (*632) [6,3]+, (632) [1+,6,3], (*333) [6,3+], (3*3)
                                                           
                   
{6,3} t0,1{6,3} t1{6,3} t1,2{6,3} t2{6,3} t0,2{6,3} t0,1,2{6,3} s{6,3} h{6,3} h1,2{6,3}
半正对偶
                                                           
                 
V6.6.6 V3.12.12 V3.6.3.6 V6.6.6 V3.3.3.3.3.3 V3.4.12.4 V.4.6.12 V3.3.3.3.6 V3.3.3.3.3.3

参见

参考文献

  1. ^ Grünbaum, Branko; and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. 
  2. ^ 《图解数学辞典》天下远见出版 复合正多边形密铺 埃里克·韦斯坦因. Demiregular Tessellation. MathWorld.