九角柱
| 此条目需要补充更多来源。 (2016年8月23日) |
在几何学中,九角柱(又称九棱柱)是一种柱体,底面为九角形。正九角柱是半正多面体、均匀多面体的一种。
 | |||
| 类别 | 棱柱 柱状均匀多面体 | ||
|---|---|---|---|
| 对偶多面体 | 双九角锥 | ||
| 数学表示法 | |||
| 考克斯特符号 | |||
| 施莱夫利符号 | t{2,9} {9}×{} | ||
| 威佐夫符号 | 2 9 | 2 | ||
| 康威表示法 | P9 | ||
| 性质 | |||
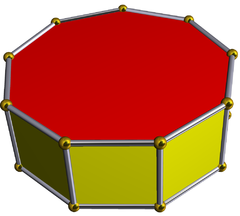
| 面 | 11 | ||
| 边 | 27 | ||
| 顶点 | 18 | ||
| 欧拉特征数 | F=11, E=27, V=18 (χ=2) | ||
| 二面角 | 90度(九边形-正方形) 140度(正方形-正方形) | ||
| 组成与布局 | |||
| 面的种类 | 2个九边形 9个矩形 | ||
| 面的布局 | 9{4}+2{9} | ||
| 顶点图 | 2.2.9 | ||
| 顶点布局 | 22.9 | ||
| 对称性 | |||
| 对称群 | D9h, [9,2], (*922), order 36 | ||
| 旋转对称群 | D9, [9,2]+, (922), order 18 | ||
| 特性 | |||
| 凸半正 | |||
| 图像 | |||
| |||
九角柱是一种十一面体,共有11个面、27条边和18个顶点[1],对偶多面体为双九角锥[2]。在其11个面中,有一组平行面,即两个面互相平行,而其他九个表面的法线在同一平面上(不一定是平行的面)。 所有平行于底面的横截面都是相同的九边形。
因为正九角柱具有对称性,且由2种正多边形组成,且每个顶点皆相等:都是2个正方形和1个正九边形的公共顶点,因此有人称正九角柱为半正十一面体。
相关多面体
九角柱是一种柱体,其他柱体有:
| 对称群 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|
| [2n,2] [n,2] [2n,2+] |
|
|
|
|
| |||||
| 图像 | |
|
|
|||||||
| 球面多面体 | ||||||||||
| 图像 | |
|
|
|
||||||
参考文献
- ^ David I. McCooey. Simplest Canonical Polyhedron with D9h Symmetry: Enneagonal Prism. [2016-08-23]. (原始内容存档于2016-08-07).
- ^ David I. McCooey. Simplest Canonical Polyhedron with D9h Symmetry: Enneagonal Dipyramid. [2022-09-14]. (原始内容存档于2022-09-14).