圆周率近似值
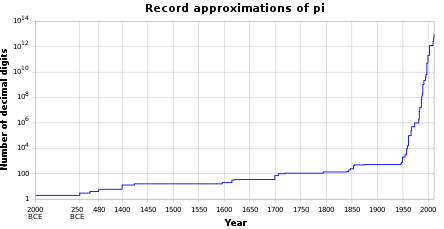
几个文明古国均在历史早期就计算出了较精确的的近似值以便于处理生产的需要。公元5世纪时,中国刘宋数学家祖冲之用几何方法将圆周率计算到小数点后7位数字。大约同一时间,印度的数学家也将圆周率计算到小数点后5位。历史上首个的精确无穷级数公式(即π的莱布尼茨公式)直到约1000年后才由印度数学家发现。[1][2]微积分的出现,很快地将的计算位数推至数百位,足以满足任何科学工程的计算需求。在20和21世纪,由于计算机技术的快速发展,借助计算机的计算使得的精度急速提高。截至2021年8月,的十进制精度已高达6.28×1013位。[3]当前人类计算的值的主要目的是为打破记录、测试超级计算机的计算能力和高精度乘法算法,因为几乎所有的科学研究对的精度要求都不会超过几百位。[4]:17[5]
近似值
经典近似值
- 整数:3
- 分数(依准确度顺序排列):22/7、333/106、355/113、52163/16604、103993/33102、245850922/78256779[6](选自 A063674 及 A063673。)
- 小数(整数后首80个位):3.14159265358979323846264338327950288419716939937510582097494459230781640628620899...[4]:240(另见 A000796)
其他进位制的近似值
- 二进制(整数后首48个位):11.001001000011111101101010100010001000010110100011...
- 十六进制(整数后首20个位):3.243F6A8885A308D31319...[4]:242
- 六十进制(整数后首5个位):3;8,29,44,0,47[7]
连分式
和所有无理数一样, 也无法表达成分数。但每个无理数包括 ,都能表达成一系列叫连分数的连续分数形式:
在这个连分数的任意一点截断化简,都能得到一个π的近似值;前四个近似值是:3, , , 。这些数在历史上是 最广为人知且广为使用的几个近似值。用以上方式得出的 的近似值要比任何有相同或更小的整数分母的其他整数分数近似值更接近π。[6]由于 是一个超越数,据超越数定义来说它不是代数数,又因此不可能是一个二次无理数;是故 不能表示为循环连分数。尽管 的简单连分数没有表现出任何其他明显规律,[8]数学家们发现了数个广义连分数能表示 ,例如:[9]
历史
远古时期
圆周率在远古时期已估算至前两位(“3”和“1”)。[谁?]
古埃及和古巴比伦
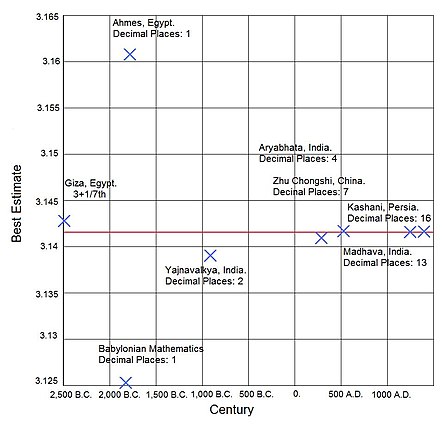
最早有记载的对圆周率估值在古埃及和古巴比伦出现,而它们两个文明古国估值都与圆周率的“精确值”相差不到百分之一,可说已是非常精准。
古埃及古王国时期时期
有不少埃及学家认为古埃及远至古王国时期时期,古埃及人已经会用 作为计算圆周率的近似值[10][注 1],但这个说法受到了质疑。[12][13][14][15]
古巴比伦
古巴比伦曾出土一块前19世纪至前16世纪的泥板,泥板上显示了人们当时把圆周率视同 ,即等于3.125。[4]:167
莱因德数学纸草书
古埃及的莱因德数学纸草书,是古埃及第二中间期时代(约前1650年)由僧侣阿姆士在纸草上抄写的一部数学著作,鉴定撰写年份为公元前1650年,但抄自一份公元前1850年的文本。它载有用作计算圆面积的公式,该公式中圆周率近似值等于 ,约等于3.1605。[4]:167
其中,古埃及的莫斯科数学纸草书,也有载有用作计算圆面积的公式,圆周率近似值等于 ,约等于3.1605。。
印度
公元前9世纪的《百道梵书》中的天文学运算把 ,约等于3.139,精确到99.91%,用作圆周率估值[16]。
而公元前6世纪的仪轨经当时采用的值是 ,约等于3.0883265。[17]
而某些公元前150年前的其他印度文献把圆周率视为 (约等于3.1622)[4]:169。
希腊的阿基米德
第一个有纪录、严谨计算π数值的算法是透过正多边形的几何算法,是由希腊数学家阿基米德在公元前250年做的。[4]:170
这个算法使用了有一千年之久,因而有时π亦称阿基米德常数。[4]:175、205
阿基米德的算法是在计算圆的外切正六边形及内接正六边形的边长,以此计算 的上限及下限,之后再将六边形变成十二边形,继续计算边长,一直计算到正96边形为止。他根据多边形的边长证明 ,也就是 。[18]
阿基米德得到的上限 也造成一个常见误解,认为 就等于 [4]:171。
希腊罗马的科学家克劳狄乌斯·托勒密在《天文学大成》一书中提到π的数值是3.1416,可能来自阿基米德,也可能来自阿波罗尼奥斯。[4]:176[19]
数学家在1630年利用多边形的方式计算π到第39位小数,一直到1699年,其他数学家才利用无穷级数的方式打破其纪录,计算到第71位小数[20]。
中国
周朝的周髀算经
在中国历史上, 的数值有3[21]、3.1547(公元前一世纪)、 (公元前100年,数值约3.1623)及 (第三世纪,数值约3.1556)[4]:176–177。
汉朝的刘歆和张衡
公元5年,汉朝的刘歆可能计算了圆周率3.1457。[22]
而一百年后,约公元130年,张衡计算了圆周率近似值 ,即约等于3.1622777。[23]
托勒密
克劳狄乌斯·托勒密,也计算了圆周率近似值为 ,也即是 。377⁄120
第一个已知的精确到小数点后三位的近似值正是托勒密做的。[24]
这个 正可用两个六十进制数字表示。
中国
三国时期吴国的王蕃
王蕃通晓天文数学。撰有《浑天图记》、《浑天象注》。曾根据浑天说和长期的天象观察,精心制作浑天仪。
他计算了圆周率近似值为 ,也即是 。
三国时期魏国的刘徽
大约在公元265年,魏国的数学家刘徽创立了割圆术,用3,072边的正多边形计算出π的数值为3.1416。[25][4]:177
刘徽后来又发明了一个较快的算法,利用边数差两倍的正多边形,其面积的差值会形成等比数列,其公比为 的原理,配合96边形 算出 的数值为3.14。[25]
六朝时期的何承天
何承天亦对圆周率进行研究,他创立了调日法,计算出圆周率近似值为111035/35329,也即约等于3.1429,准确至小数点后2位[26]。
六朝时期的祖冲之
据《隋书·律历志》[27]记载,祖冲之以“以直径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间。密率,圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二。”,以此为直径求圆周率,求得盈数(即过剩的近似值)为 ;肭数(即不足的近似值)为 ,圆周率的真值介于盈肭两数之间。
《隋书》没有具体说明祖冲之是用什么方法计算出盈肭两数的。一般认为,祖冲之采用的是刘徽割圆术分割到24576边形,又用刘徽圆周率不等式得祖冲之著名的圆周率不等式: 。
祖冲之的这一结果精确到小数点后第7位,直到一千多年后才由15世纪的阿拉伯数学家阿尔·卡西以17位有效数字打破此记录[28]。
按照当时计算使用分数的习惯,祖冲之还采用了两个分数值的圆周率:“约率” (或称之为“疏率”[注 2])以及“密率” 。在分母<16600的所有整分数中,密率的比值最接近圆周率[注 3]。祖冲之可能利用何承天的调日法求得圆周率的约率和密率[30]。数学家华罗庚曾认为密率的求得,说明祖冲之可能已经掌握了连分数的概念。
日本数学家三上义夫说,“约率 ,无非是几百年前希腊数学家阿基米德已经得到的数值,但是 这个分数,却是翻遍古希腊,古印度和阿拉伯的数学文献都找不到的分数,希腊人肯定不知道它;在欧洲直到1586年才由荷兰人安托尼斯宗(Adriaan Anthoniszoon)求出了 这个比值。因此,中国人掌握这个非凡的圆周率分数比欧洲早出整整一千年之久”。为纪念这位伟大的中国古代数学家,三上义夫要求把 称为“祖率”[31]。
祖冲之在公元480年利用割圆术计算12,288形的边长,得到 的值在3.1415926和3.1415927之间。在之后的八百年内,这都是准确度最高的π估计值。[4]:178为纪念祖冲之对圆周率发展的贡献,日本数学家三上义夫将这一推算值命名为“祖冲之圆周率”,简称“祖率”。[32]
印度
阿耶波多
印度天文学家阿耶波多在公元499年的著作《阿里亚哈塔历书》中使用了3.1416的数值。[4]:179
婆罗摩笈多
计算出出 ,也即约等于3.1622777。
斐波那契
斐波那契在大约1220年利用独立于阿基米德多边形法,计算出3.1418[4]:180。
意大利的但丁·阿利吉耶里
意大利作家但丁·阿利吉耶里则计得 。[4]:180
波斯的卡西
波斯天文学家卡西在1424年利用3×228边的多边形,计算到六十进制的第9位小数,相当十进制的第16位小数。[33][34]这一突破成为当时的纪录,延续了约180年。[35]
法国的弗朗索瓦·韦达
法国的数学家弗朗索瓦·韦达在1579年用3×217边形计算到第9位小数[35]。
阿德里安·范·罗门
阿德里安·范·罗门在1593年计算到第15位小数[35]。
荷兰的鲁道夫·范·科伊伦
荷兰数学家鲁道夫·范·科伊伦在1596年计算到第20位小数,他之后又计算到第35位小数,因此在二十世纪初之前,圆周率在德国会称为鲁道夫数。[4]:182–183
荷兰的威理博·司乃耳
荷兰科学家威理博·司乃耳在1621年计算到第34位小数[4]:183。
奥地利的克里斯托夫·格林伯格
奥地利天文学家克里斯托夫·格林伯格在1630年用1040边形计算到第38位小数[36],至今这仍是利用多边形算法可以达到最准确的结果[4]:183。
无穷级数
16世纪及17世纪时, 的计算开始改用无穷级数的计算方式。无穷级数是一组无穷数列的和[4]:185–191。
无穷级数让数学家可以计算出比阿基米德以及其他用几何方式计算的数学家更准确的结果。[4]:185–191
虽然詹姆斯·格雷果里及戈特弗里德·莱布尼茨等欧洲数学家利用无穷数列计算π而使得该方法为大家所知,但这种方法最早是由印度科学家在大约1400到1500年之间发现的。[4]:185-186[37]第一个记载的用无穷级数计算π的人是约公元1500年左右时,印度天文学家尼拉卡莎·萨默亚士在他的著作《系统汇编》中用梵语诗所记录。[38]当时没有这个数列对应的证明,而证明出现在另一本较晚的印度作品《基本原理》,年代约在公元1530年。尼拉卡莎将该数列归功于更早期的印度数学家桑加马格拉马的马德哈瓦( 1350 – 1425)。[38]有许多相关的无穷级数,包括有关 、 及 的,现在称为马德哈瓦数列或π的莱布尼茨公式[38]。玛达瓦在1400年用无穷级数计算π到第11位小数,但在1430年一位波斯数学家卡西利用多边形算法否定了他算的的结果[39]。
欧洲第一个发现的无穷项圆周率公式是无穷乘积(和一般用来计算π的无穷级数不同),由法国科学家弗朗索瓦·韦达在1593年发现[4]:187[41]:
约翰·沃利斯在1655年发现了沃利斯乘积,是欧洲第二个发现的无穷项圆周率公式[4]:187:
微积分学是由英国科学家艾萨克·牛顿及德国数学家戈特弗里德·莱布尼茨在1660年代发明,因此也出现许多计算π的无穷级数。牛顿自己就利用反正弦( )数列在1655年或1666年将π近似到第15位小数,后来写到“我很羞愧的告诉你我为了这个计算用了多少个数字,我当时没有做其他的事。”[40]
苏格兰数学家詹姆斯·格雷果里在1671年发现了马德哈瓦公式,莱布尼茨也在1674年发现:[4]:188–189[42]
这个公式即为格雷果里-莱布尼茨公式,在 时数值为 。[42]1699年时英国数学家亚伯拉罕·夏普用格雷果里-莱布尼茨公式,在 时计算,计算到了 的第71位小数,打破由多边形算法得到的第39位小数的记录。[4]:189格雷果里-莱布尼茨公式在 时非常简单,但收敛到最终值的速度非常慢,因此现在不再会用此公式来计算 。[4]:156
约翰·梅钦在1706年利用格雷果里-莱布尼茨级数产生了一个可以快速收敛的公式:[4]:192–193
梅钦用这个公式计算到 的第100位小数[4]:72–74后来其他数学家也发展了一些类似公式,现在称为梅钦类公式,创下了许多计算 位数的记录。[4]:72–74在进入电脑时代时,梅钦类公式仍然是个耳熟能详的可以计算 的公式,而且在约250年的时间里,很多有关 位数的记录都是梅钦类公式所得,比如在1946年时由达尼尔·弗格森(Daniel Ferguson)用这类公式计算到第620位小数,是在没有计算设备辅助下的最佳纪录。[4]:192–196, 205
1844年,计算天才扎卡里亚斯·达斯在德国数学家卡尔·弗里德里希·高斯的要求下以梅钦类公式心算了 的200个小数位,并创下纪录。[4]:194-196英国数学家威廉·谢克斯花了15年的时间计算π到小数707位,不过中间在第528位小数时出错,因此后面的小数也都不正确。[4]:194–196
收敛速度
有些π的无穷级数收敛的比其他级数要快,数学家一般会选用收敛速度较快的级数,可以在较少的计算量下计算 ,且达到需要的准确度[43][4]:15–17, 70–72, 104, 156, 192–197, 201–202。以下是π的莱布尼茨公式:[4]:69–72
随着一项一项的值加入总和中,只要项次够多,总和最后会慢慢接近 。不过此数列的收敛速度很慢,要到500,000项之后,才会精确到 的第五小数[44]。
尼拉卡莎在15世纪发展了另一个 的无穷级数,其收敛速度较格雷果里-莱布尼茨公式要快很多,该级数为:[45]
以下比较二个级数的收敛速率:
| 的无穷级数 | 第1项 | 前2项 | 前3项 | 前4项 | 前5项 | 收敛到: |
|---|---|---|---|---|---|---|
| 4.0000 | 2.6666... | 3.4666... | 2.8952... | 3.3396... | π = 3.1415... | |
| 3.0000 | 3.1666... | 3.1333... | 3.1452... | 3.1396... |
计算前5项后,格雷果里-莱布尼茨级数的和跟 的误差为0.2,而尼拉卡莎级数和的误差为0.002。尼拉卡莎级数收敛的快很多,因此也比较适合用来计算 的数值。收敛更快的级数有梅钦类公式及楚德诺夫斯基算法,后者每计算一项就可以得到14位正确的小数值数[43]。
计算机时代与迭代算法
二十世纪中期计算机技术的发展、革新再次引发了计算π位数的热潮。美国数学家约翰·伦奇及李维·史密斯在1949年利用桌上型计算机计算到1,120位[4]:205。同年,乔治·韦斯纳(George Reitwiesner)及约翰·冯·诺伊曼带领的团队利用反三角函数(arctan)的无穷级数,通过ENIAC计算到了小数第2,037位,花了70小时的电脑工作时间[46]。这一纪录后来多次由其他透过arctan级数计算出的结果打破(1957年到7480位小数,1958年到第一万位数,1961年到第十万位小数),直到1973年,人们计算出了小数点后的第一百万位小数[4]:197。
1980年代的两项发明加速了 的计算。第一项是人们发现了新的的迭代法去计算π的值,其计算速度比无穷级数会要快很多。另一项是人们发现了可以快速计算大数字乘积的乘法算法[4]:15–17。这类算法在现代π的计算上格外的重要,因为电脑大部分的工作时间都是在计算乘法[4]:131。这类算法包括Karatsuba算法、Toom–Cook乘法及以傅里叶变换为基础的乘法算法(傅里叶乘法)[4]:132, 140。
迭代算法最早是在1975年至1976年间分别由美国物理学家尤金·萨拉明及奥地利科学家理查·布兰特独立提出[4]:87。这两个算法没有依赖无穷级数来计算。迭代会重复一个特定的计算,将前一次的计算结果作为这一次的输入值,使得计算结果渐渐的趋近理想值。此方式的原始版本其实是在160年前由卡尔·弗里德里希·高斯提出,现在称为算术-几何平均数算法(AGM法)或高斯-勒让德算法[4]:87。因为萨拉明及布兰特都曾对此进行修改,因此这个算法也称为萨拉明-布兰特算法。
迭代算法因为收敛速度比无穷级数快很多,在1980年代以后广为使用。无穷级数随着项次的增加,一般来说正确的位数也会增加几位,但迭代算法每多一次计算,正确的位数会呈几何级数增长。例如萨拉明-布兰特算法每多一次计算,正确位数会是之前的二倍。1984年加拿大人乔纳森·波温及彼得·波温提出一个迭代算法,每多一次计算,正确位数会是之前的四倍,1987年时有另一个迭代算法,每多一次计算,正确位数会是之前的五倍[47]。日本数学家金田康正使用的算法在1955年及2002年之间创下了若干个纪录[48]。不过迭代算法的快速收敛也有其代价,因为这个算法需要的内存的大小明显的要比无穷级数要多[48]。
计算 的意义
一般而言, 值并不需要过于精确便能够满足大部分的数学运算的需求。按照约尔格·阿恩特(Jörg Arndt)及克里斯托夫·黑内尔(Christoph Haenel)的计算,39个数位已足够运算绝大多数的宇宙学的计算需求,因为这个精确度已能够将可观测宇宙圆周的精确度准确至一个原子大小[49]。 尽管如此,人们仍然是奋力地运算出 小数点后的上千甚至上百万个数位[4]:17–19。这一部分是出于人类对打破记录的冲动,因为那些和 有关的成就往往成为世界各地的新闻头条[50][51]。此外,这其中也有一些实际的好处,例如测试超级计算机、测试数值分析算法等(包括高精度乘法算法)。在纯粹数学的领域中,计算 的位数也能让人们来评定π的随机性[4]:18。
快速收敛级数
现代计算 的程序不仅仅局限于迭代算法。20世纪80与90年代,人们发现了一些可用来计算 的新无穷级数,其收敛速度可与迭代算法媲美,而又有着复杂度、内存密集度更低的优势。[48]印度数学家斯里尼瓦瑟·拉马努金是这方面的先驱,他在1914年发表了许多与 相关的公式,这些公式十分新颖,极为优雅而又颇具数学深度,收敛速度也非常快。[4]:103–104下式即为一例,其中用到了模方程:
这个无穷级数收敛速度远快于绝大多数反正切数列,包括梅钦公式。[4]:104第一位使用拉马努金公式计算 并取得进展的是比尔·高斯珀,他在1985年算得了小数点后一千七百万位。[4]:104, 206拉马努金公式开创了现代数值近似算法的先河,此后波尔文兄弟和楚德诺夫斯基兄弟进一步发展了这类算法。[4]:110–111后者于1987年提出了楚德诺夫斯基公式,如下所示:
此公式每计算一项就能得到 的约14位数值[52],因而用于突破圆周率的数位的计算。利用这个公式,楚德诺夫斯基兄弟于1989年算得 小数点后10亿(109)位,法布里斯·贝拉于2009年算得2.7千亿(2.7×1012)位,亚历山大·易和近藤滋在2011年算得一万亿(1013)位。[4]:110–111, 206[53][54]类似的公式还有拉马努金-佐藤级数。
2006年,加拿大数学家西蒙·普劳夫利用PSLQ整数关系算法[55]按照以下模版生成了几个计算 的新公式:
其中 为e , 是一个奇数, 是普劳夫计算出的有理常数。[56]
蒙特卡洛方法
蒙特卡洛方法是以概率统计理论为指导的一类非常重要的数值计算方法,通过进行大量重复试验计算事件发生的频率,按照大数定律(即当试验次数充分大时,频率充分地接近于概率)可以求得 的近似值[57]。 布丰投针问题就是其中一个应用的例子:当一枚长度为 的针随机地往一个画满间距为 的平行线的平面上抛掷 次, 如果针与平行直线相交了 次,那么当 充分大时就可根据以下公式算出 的近似值[58]:
另一个利用蒙特卡罗方法计算 值的例子是随机地往内切四分之一圆的正方形内抛掷大量的点,落在四分之一圆内的点的数量与抛掷点的总量的比值会近似等于 .[4]:39–40[59]
此外,还可以通过进行随机游走试验,并利用蒙特卡罗方法计算 值,如抛掷一枚均匀的硬币 次,并记录正面朝上的次数,所得结果中,正面朝上的次数 服从二项分布且
因为硬币均匀,所以N次试验中每次试验结果相互独立。由此可定义一系列独立的随机变量 ,当抛掷结果为正面时 否则为-1,且 且取何值具有相同的概率(即,正面朝上和背面朝上的概率相同)。对随机变量 求和可得
设k为“硬币正面朝上的次数”减去“硬币反面朝上的次数”,即可得到 。对式子进行变换,得 ,因此
- ,其中 。
可以证明[60],
- , ,以及
并且当 变大时, 的值会渐近于 ,因此当 充分大时可根据以下公式算出 的近似值:[61]
和其他计算 值的方法相比,蒙特卡洛方法收敛速度很慢,而且无论进行多少次实验,都无从得知 的估值已经精确到了第几位。因此,当追求速度或精度时,蒙特卡洛方法不适合用来估计 。[4]:43[62]
阀门算法
1995年引入的两个算法开辟了研究 的新途径。因为每计算出一位数字,该数就会像流过阀门的水一样不会再出现在后续的计算过程中,这种新进算法叫做阀门算法。[4]:77–84[63]这就与无穷级数及迭代算法形成对比——无穷级数和迭代算法自始至终的每一步计算都会涉及到之前所有步骤计算出的中间值。[4]:77–84
1995年,美国数学家斯坦·瓦格纳和斯坦利·拉比诺维茨(Stanley Rabinowitz)发明了一种简单的阀门算法[63][4]:77[64],其运算速度类似arctan算法,但速度比迭代算法要慢[4]:77。
贝利-波尔温-普劳夫公式(BBP)是另一个阀门算法,属于一种位数萃取算法。1995年,西蒙·普劳夫等人发现[4]:117, 126–128[65]
这个公式和其他的公式不同,可以在十六进制下计算 的任意位数小数,而不用计算所有前面的小数位数[4]:117, 126–128。一个十六进制下的数位可计算得到特定一个二进制的数位;想要得到一个八进制数位的话,计算一、两个十六进制小数即可。目前也已发现一些这种算法的变体,不过人们还没有发现针对十进制、可以快速产生特定位数小数数字的位数萃取算法[66]。位数萃取算法的一个重要用途是用来确认声称是计算到 小数位数的新记录:若有声称是新纪录的计算结果出现,先将十进制的数值变换到十六进制,再用贝利-波尔温-普劳夫公式,去确认最后的一些位数(用乱数决定),若这些位数都对,人们就能有一定把握认为此计算结果是对的[54]。
在1998年到2000年之间,分布式计算计划PiHex利用贝拉公式(贝利-波尔温-普劳夫公式的一种变体)计算 的第1015个位,结果是0[4]:20[67]。在2010年9月,一名雅虎员工利用公司的Apache Hadoop应用程序在上千台电脑上计算 在2×1015个数位开始,往后数的256个位,其第2×1015个位刚好也是0[68]。
趣闻
值得注意的是,一些法律或历史文本欲“定义π”为有理数,尤其是1897年的“印第安纳州法案”,指明“直径和圆周比例为四分之五比4(暗示“π= 3.2”);和希伯来圣经中的一个段落,暗示“π= 3”。
圣经估算的价值
印第安纳州法案
计算圆周率近似值的方程的发展
梅钦类公式(Machin-like formulae)
其他古代公式
现代公式
二进制数位公式
π和一个分形
多方面的近似值
在古代,人们使用60进制来计算。在60进制中,π能被准确至小数点后八位(十进制),而这数字是3:8:29:4460,即是:
(下一个60进制的数位为0)
除此之外,π的近似值还能以以下方式表示:
- 准确至3位:
- 准确至4位:
- 准确至4位:
- 拉马努金的近似值,准确至4位:
- 准确至5位:
- 准确至7位:
- 拉马努金的近似值,准确至7位:
- 由前述无穷级数仅取第1项即得
- 准确至9位:
- 这是拉马努金提出的,拉马努金说他在梦中收到印度神Namagiri的启示。[71]
- 准确至10位:
- 准确至10位:
- 准确至18位:
- 准确至30位:
圆形的面积
可以通过蒙特卡洛方法来计算圆周率 。
以原点(0, 0)为圆心,画一个半径为 的圆。然后以原点为中心,画一个边长为 的正方形。圆和正方形内切。
圆的面积为 ,正方形的面积为 。
于是有, 。
通过生成0到r之间随机数作为一个点的横纵坐标,所有点均落在正方形内。
通过统计圆内的点数 与总点数 , 。
当随时点的数目增加时,所得结果会越接近于圆周率。
但是该方法也有不足之处。具体可参考蒙特卡洛方法。
以正多边形来计算π的值
连分数
π的连分数表示式是[3; 7, 15, 1, 292, 1, 1, ...]。这连分数没有任何模式。π有很多用一条简单的规矩然制成的广义连分数
(其他连分数能在这里(页面存档备份,存于互联网档案馆)查看。)
三角函数
莱布尼茨公式
反正切
反正弦
萨拉明 - 布伦特公式
计算任意数位的方法
在1995年,西蒙·普劳夫发现了贝利-波尔温-普劳夫公式。这公式能在16进制中计算pi的任意数位,而不用计算之前的数位。[73]
在1996年,西蒙·普劳夫发明了一个公式,能在O(n3log(n)3)的时间之内计算出pi在任意进制的第n个数位[74]。在1997年,法布里斯·贝拉发明了另一个公式,把计算所需时间缩短至O(n2)。他又发明了在2进制计算pi的公式。[75]
有效的方法
在1961年,丹尼尔柄和他的团队在美国海军研究实验室计算了π的前100,000数位。
他和他的团队使用了两个不同的幂级数来计算π的数值。第一个幂级数中,任何错误都会造成一个比较高的数值;而另一个中,任何错误都会造成一个比较低的数值。所以如果两个幂级数计算出同样的数值,那个数值就肯定正确。美国海军研究实验室发放了π的前100,000数位。
但是以上的两个幂级数也要很长的时间才能计算出结果。相反地,约翰·梅钦的公式与反正切的泰勒级数一起使用则能很快地计算结果:
使用复数的极坐标系便能证实这公式,以以下的数学式开始:
这类的公式被称为梅钦类公式。(注意,{ x,y} = {239, 132}是佩尔方程“x2-2y2 = -1”的其中一个解答。)
印度数学家斯里尼瓦瑟·拉马努金发现了π的很多其他表示方式。他与戈弗雷·哈罗德·哈代一起工作了很多年。
如果要计算π小数点后很多位,计算者通常会使用高斯-勒让德算法,波尔温公式,和1976年发明的萨拉明 - 布伦特公式。
π和1/π的小数点后首十万位能在古腾堡计划里查阅(参见#外部链接)。
在2002年12月,在东京大学进修的金田康正发放了π小数点后1,241,100,000,000位的值,创造了新的世界记录。他在2002年9月以六十四部日立的超级电脑计算出这值。这些电脑有1TB的内存,而且能在每秒执行2兆次运算。上一个记录(21亿位)所使用的电脑每秒只能执行1兆次运算。金田康正使用了以下公式:
- K. Takano (1982).
- F. C. W. Störmer (1896).
这些近似值由于有太多数位,所以没有实际用途,只是用来测试超级电脑。
在1997年,大卫·贝利(David H. Bailey)、皮特·波尔温和西蒙·普劳夫发布了一条新的公式来计算π的值:
这公式能在不知道前k - 1数位的值之下,在2进制或16进制中计算出π的第k个数位的值。贝利的网页(页面存档备份,存于互联网档案馆)包含了计算方法,而且把方法以几个编程语言记下。PiHex计算出π小数点后一兆数位的值。
法布里斯·贝拉推出了贝利-波尔温-普劳夫公式的改良版——贝拉公式:
还有其他计算π的值的公式:
拉马努金的公式收敛的速度异常地快,这公式后来在2000年演变成最快的公式(楚德诺夫斯基算法):
- David Chudnovsky和Gregory Chudnovsky.
关于圆周率近似值的计划
计算圆周率近似值的软件
General purpose
大多数计算机代数系统可以计算出π和其他常见的数学常数到任何所需的精度。
计算π的功能中还包括许多通用库任意精度算术运算,例如CLN和MPFR。
注释
参考资料
- ^ George E. Andrews, Richard Askey, Ranjan Roy. Special Functions. Cambridge University Press. 1999: 58. ISBN 0-521-78988-5.
- ^ Gupta, R. C. On the remainder term in the Madhava–Leibniz's series. Ganita Bharati. 1992, 14 (1-4): 68–71.
- ^ 62.8万亿个数字:瑞士大学创造了新的圆周率计算记录. [2021-08-20]. (原始内容存档于2021-08-26) (中文).
- ^ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 4.12 4.13 4.14 4.15 4.16 4.17 4.18 4.19 4.20 4.21 4.22 4.23 4.24 4.25 4.26 4.27 4.28 4.29 4.30 4.31 4.32 4.33 4.34 4.35 4.36 4.37 4.38 4.39 4.40 4.41 4.42 4.43 4.44 4.45 4.46 4.47 4.48 4.49 4.50 4.51 4.52 4.53 4.54 4.55 4.56 4.57 Arndt & Haenel 2006
- ^ David Bailey; Jonathan Borwein; Peter Borwein; Simon Plouffe, The Quest for Pi, The Mathematical Intelligencer, 1997, 19 (1): 50–56, doi:10.1007/bf03024340
- ^ 6.0 6.1 Eymard & Lafon 1999,第78页
- ^ Kennedy, E. S., Abu-r-Raihan al-Biruni, 973-1048, Journal for the History of Astronomy: 65, Bibcode:1978JHA.....9...65K, doi:10.1177/002182867800900106。克劳狄乌斯·托勒密使用了60进制下的三位小数去近似,随后卡西将其扩展到了九位小数。参见Aaboe, Asger, Episodes from the Early History of Mathematics, New Mathematical Library 13, 纽约: Random House: 125, 1964 [2017-12-08], (原始内容存档于2017-02-01)
- ^ Sloane, N.J.A. (编). Sequence A001203 (Continued fraction for Pi). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 12 April 2012.
- ^ Lange, L. J. An Elegant Continued Fraction for π. The American Mathematical Monthly. 1999-05, 106 (5): 456–458. JSTOR 2589152. doi:10.2307/2589152.
- ^ Petrie, W.M.F. Wisdom of the Egyptians (1940)
- ^ Verner, Miroslav. The Pyramids: The Mystery, Culture, and Science of Egypt's Great Monuments. Grove Press. 2001 (1997). ISBN 0-8021-3935-3
- ^ Rossi, Corinna Architecture and Mathematics in Ancient Egypt, Cambridge University Press. 2007. ISBN 978-0-521-69053-9.
- ^ Legon, J. A. R. On Pyramid Dimensions and Proportions (1991) Discussions in Egyptology (20) 第25-34页 [1] (页面存档备份,存于互联网档案馆)
- ^ "We can conclude that although the ancient Egyptians could not precisely define the value of π, in practice they used it". Verner, M. The Pyramids: Their Archaeology and History. 2003.,第70页。
Petrie. Wisdom of the Egyptians. 1940.,第30页。
参见Legon, J. A. R. On Pyramid Dimensions and Proportions. Discussions in Egyptology. 1991, 20: 第25–34页 [2016-09-13]. (原始内容存档于2011-07-18)..
参见Petrie, W. M. F. Surveys of the Great Pyramids. Nature. 1925, 116 (2930期): 第942页. Bibcode:1925Natur.116..942P. doi:10.1038/116942a0. - ^ Egyptologist: Rossi, Corinna, Architecture and Mathematics in Ancient Egypt, Cambridge University Press, 2004, 第60-70页,200, Shermer, Michael), The Skeptic Encyclopedia of Pseudoscience, ABC-CLIO, 2002, 第407-408页, ISBN 9780889203242. (原始内容存档于2016-11-29).
- ^ Chaitanya, Krishna. A profile of Indian culture. (页面存档备份,存于互联网档案馆) Indian Book Company (1975). 第133页。
- ^ Arndt & Haenel 2006,第168–169页
- ^ The Computation of Pi by Archimedes: The Computation of Pi by Archimedes – File Exchange – MATLAB Central. Mathworks.com. [2013-03-12]. (原始内容存档于2013-02-25).
- ^ Boyer & Merzbach 1991,第168页
- ^ Arndt & Haenel 2006,第15–16, 175, 184–186, 205页Grienberger在1630年已计算到39位小数,Sharp在1699年计算到71位小数
- ^ 《周髀算经》注中, 赵爽指出“圆径一而周三,方径一而匝四”。
- ^ 《π和e》,夏道行,商务印书馆,第10页,ISBN 962-07-2007-5
- ^ 吴文俊主编 《中国数学史大系》 第三卷 第一编 第二节 张衡的数学研究 第5页
- ^ 25.0 25.1 Boyer & Merzbach 1991,第202页
- ^ 李俨 《中国古代数学史料》 中国科学图书仪器公司 12.《中国古代数学家》 64页
- ^ 隋书/卷16
- ^ 吴文俊 主编 《中国数学史大系》副卷第一卷 480页 ISBN 9787030146359.
- ^ 吴文俊 主编 《中国数学史大系》第四卷 123页 ISBN 7-300-0425-8/O
- ^ “We are on this account strongly urged to express a desire that it should henceforth be called by the name of Tsu Ch'ong-chih's fractional value for π” Yoshio Mikami, Development of Mathematics in China and Japan p50 1913 Leipzig
- ^ 此零非彼O. 台湾商务印书馆. 2006: 286. ISBN 978-957-05-2072-9.
- ^ Azarian, Mohammad K. al-Risāla al-muhītīyya: A Summary. Missouri Journal of Mathematical Sciences. 2010, 22 (2): 64–85 [2016-09-13]. (原始内容存档于2015-01-14).
- ^ O'Connor, John J.; Robertson, Edmund F. Ghiyath al-Din Jamshid Mas'ud al-Kashi. MacTutor History of Mathematics archive. 1999 [2012-08-11]. (原始内容存档于2011-04-12).
- ^ 35.0 35.1 35.2 Arndt & Haenel 2006,第182页
- ^ Grienbergerus, Christophorus. Elementa Trigonometrica (PDF). 1630 [2016-09-13]. (原始内容 (PDF)存档于2014-02-01) (拉丁语).。其计算结果是3.14159 26535 89793 23846 26433 83279 50288 4196 < π < 3.14159 26535 89793 23846 26433 83279 50288 4199
- ^ Roy 1990,第101–102页
- ^ 38.0 38.1 38.2 Roy 1990,第101–102页
- ^ Joseph 1991,第264页
- ^ 40.0 40.1 Arndt & Haenel 2006,第188页. 牛顿由Arndt引用。
- ^ A060294
- ^ 42.0 42.1 Eymard & Lafon 1999,第53–54页
- ^ 43.0 43.1 Borwein, J. M.; Borwein, P. B. Ramanujan and Pi. Scientific American. 1988, 256 (2): 112–117. Bibcode:1988SciAm.258b.112B. doi:10.1038/scientificamerican0288-112.
- ^ Borwein, J. M.; Borwein, P. B.; Dilcher, K. Pi, Euler Numbers, and Asymptotic Expansions. American Mathematical Monthly. 1989, 96 (8): 681–687. doi:10.2307/2324715.
- ^ Arndt & Haenel 2006,第223页, (formula 16.10). Note that (n − 1)n(n + 1) = n3 − n.
Wells, David. The Penguin Dictionary of Curious and Interesting Numbers revised. Penguin. 1997: 35. ISBN 978-0-140-26149-3. - ^ Arndt & Haenel 2006,第197页。参见 Reitwiesner 1950.
- ^ Arndt & Haenel 2006,第第111页(5 倍);第113–114(4 倍)页.
具体算法情参见Borwein & Borwein 1987。 - ^ 48.0 48.1 48.2 Bailey, David H. Some Background on Kanada’s Recent Pi Calculation (PDF). 2003-05-16 [2012-04-12]. (原始内容存档 (PDF)于2012-04-15).
- ^ Arndt & Haenel 2006,第17页“39 digits of are sufficient to calculate the volume of the universe to the nearest atom.”(中文:39位 已经足以计算宇宙到其最近的原子的体积了。)
鉴于人们需要一些额外的数位来解决舍入误差的问题,阿恩特称几百位小数足以应付任何科学计算了。 - ^ Schudel, Matt. John W. Wrench, Jr.: Mathematician Had a Taste for Pi. The Washington Post. 2009-03-25: B5.
- ^ Connor, Steve. The Big Question: How close have we come to knowing the precise value of pi?. The Independent (London). 2010-01-08 [2012-04-14]. (原始内容存档于2012-04-02).
- ^ Eymard & Lafon 1999,第254页
- ^ Fabrice Bellard. Computation of 2700 billion decimal digits of Pi using a Desktop Computer - Semantic Scholar. www.semanticscholar.org. 2010-02-11 [2017-04-10].
- ^ 54.0 54.1 Pi - 12.1 Trillion Digits. www.numberworld.org. [2012-05-30]. (原始内容存档于2014-01-01).
- ^ PSLQ即Partial Sum of Least Squares,偏最小二乘和。
- ^ Plouffe, Simon. Identities inspired by Ramanujan's Notebooks (part 2) (PDF). 2006-04 [2009-04-10]. (原始内容存档 (PDF)于2012-01-14).
- ^ 苏淳, 概率论 2nd, 北京: 科学出版社: 41, 2010
- ^ 苏淳, 概率论 2nd, 北京: 科学出版社: 34–35,41, 2010
- ^ Posamentier & Lehmann 2004,第105页
- ^ Weisstein, Eric W. (编). Random Walk--1-Dimensiona. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2016-09-18]. (原始内容存档于2016-11-18) (英语).
- ^ Grünbaum, B., Projection Constants, Trans. Amer. Math. Soc., 1960, 95: 451–465
- ^ Posamentier & Lehmann 2004,第105–108页
- ^ 63.0 63.1 Gibbons, Jeremy, "Unbounded Spigot Algorithms for the Digits of Pi" (页面存档备份,存于互联网档案馆), 2005. Gibbons produced an improved version of Wagon's algorithm.
- ^ Rabinowitz, Stanley; Wagon, Stan. A spigot algorithm for the digits of Pi. American Mathematical Monthly. 1995-03, 102 (3): 195–203. doi:10.2307/2975006. A computer program has been created that implements Wagon's spigot algorithm in only 120 characters of software.
- ^ Bailey, David H; Borwein, Peter B; and Plouffe, Simon. On the Rapid Computation of Various Polylogarithmic Constants (PDF). Mathematics of Computation. 1997-04, 66 (218): 903–913 [2016-09-13]. doi:10.1090/S0025-5718-97-00856-9. (原始内容存档 (PDF)于2012-07-22).
- ^ Arndt & Haenel 2006,第128页。普劳夫有找到十进制的位数萃取算法,但其速度比完整计算之前所有位数要慢。
- ^ Bellards formula in: Bellard, Fabrice. A new formula to compute the nth binary digit of pi. [2007-10-27]. (原始内容存档于2007-09-12).
- ^ Palmer, Jason. Pi record smashed as team finds two-quadrillionth digit. BBC News. 2010-09-16 [2011-03-26]. (原始内容存档于2011-03-17).
- ^ A nested radical approximation for pi (PDF). [2013-02-18]. (原始内容 (PDF)存档于2011-07-06).
- ^ Gardner, Martin. New Mathematical Diversions. Mathematical Association of America: 92. 1995..
- ^ "Lost notebook page 16" ,Ramanujan
- ^ CetinHakimoglu–Brown. [2013-02-18]. (原始内容存档于2009-03-29).
- ^ Weisstein, Eric W. (编). BBP Formula. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (原始内容存档于2010-02-25) (英语).
- ^ Simon Plouffe, On the computation of the n'th decimal digit of various transcendental numbers, November 1996
- ^ Bellard's Website:Bellard.org (页面存档备份,存于互联网档案馆)